| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 4 Quadratic Equations
This solutions guide is dedicated to Chapter 4: Quadratic Equations, a significant progression in algebra that moves beyond the linear relationships explored previously. Quadratic equations, characterized by the presence of a variable term raised to the power of two, represent a fundamental class of polynomial equations with widespread applications in various fields, including physics (e.g., projectile motion), engineering (e.g., designing parabolic structures), economics (e.g., modeling profit), and pure mathematics. Understanding how to effectively solve these equations and analyze the nature of their solutions, often referred to as roots, is a critical skill. These roots represent the specific values of the variable that satisfy the equation, making the expression equal to zero. Geometrically, for an equation like $y = ax^2 + bx + c$, the real roots correspond to the x-intercepts of its parabolic graph. This chapter systematically introduces and explains the standard form of quadratic equations, explores various powerful techniques for finding their roots, and delves into methods for determining the type of roots an equation possesses without necessarily calculating them explicitly. The transition from merely identifying a quadratic equation to mastering its solution techniques and interpreting the results forms the core objective of this chapter's study.
The journey begins by firmly establishing the standard form of a quadratic equation: $ax^2 + bx + c = 0$, where $a$, $b$, and $c$ are real coefficients, and crucially, $a \neq 0$ (if $a$ were zero, the equation would become linear). The solutions first guide students in identifying whether a given algebraic equation can be simplified into this standard form, thus classifying it as quadratic. They also demonstrate how to translate various real-world scenarios and word problems into the language of quadratic equations, setting the stage for solving them.
Finding the roots is the central task, and the solutions detail three principal algebraic methods:
- Factorization: This method involves rewriting the quadratic polynomial $ax^2 + bx + c$ as a product of two linear factors, say $(px+q)(rx+s)$. This is often achieved by techniques like "splitting the middle term" (finding two numbers whose product is $ac$ and whose sum is $b$) or by recognizing and applying standard algebraic identities. Once factored, the equation becomes $(px+q)(rx+s) = 0$. Since the product is zero, at least one of the factors must be zero, leading to $px+q=0$ or $rx+s=0$, which are simple linear equations yielding the roots.
- Completing the Square: This powerful technique transforms the standard quadratic equation into the form $(x+k)^2 = m$ by algebraic manipulation. The solutions provide a step-by-step guide: moving the constant term, dividing by $a$ (if $a \neq 1$), adding the square of half the coefficient of the $x$ term to both sides to create a perfect square trinomial, and then taking the square root of both sides to solve for $x$. While sometimes computationally more involved than factorization, this method works for all quadratic equations and provides the theoretical basis for the quadratic formula.
- Quadratic Formula: Derived directly from the method of completing the square, the quadratic formula offers a universal, direct approach to finding the roots of any quadratic equation $ax^2 + bx + c = 0$. The formula is given by: $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$. The solutions demonstrate its straightforward application, requiring only the identification of coefficients $a, b,$ and $c$.
Beyond finding the roots, understanding their nature is crucial. This is determined by the value of the discriminant, denoted by $D$, which is the expression under the square root in the quadratic formula: $D = b^2 - 4ac$. The solutions explain the interpretation of the discriminant:
- If $D > 0$: The equation has two distinct real roots ($\frac{-b + \sqrt{D}}{2a}$ and $\frac{-b - \sqrt{D}}{2a}$).
- If $D = 0$: The equation has two equal real roots (or one distinct real root), given by $x = -\frac{b}{2a}$.
- If $D < 0$: The equation has no real roots (the roots are complex conjugates, typically studied in higher classes).
Solutions demonstrate how to calculate $D$ and use its sign to predict the nature of the roots without needing to compute the roots themselves.
Finally, the chapter application is reinforced through numerous word problems. These cover diverse contexts such as finding dimensions of geometric areas, solving age-related problems, calculating speeds and times in motion problems, finding consecutive integers with specific properties, and more. The solutions provide meticulous guidance on formulating the quadratic equation that models the given situation and then solving it using an appropriate method, ensuring that the final answer is relevant and valid within the context of the original problem (e.g., rejecting negative lengths or ages).
Example 1 & 2 (Before Exercise 4.1)
Example 1. Represent the following situations mathematically:
(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.
(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was ₹ 750. We would like to find out the number of toys produced on that day.
Answer:
Solution (i)
To Find: Mathematical representation of the situation.
Solution:
Let the number of marbles John had initially be $x$.
Since John and Jivanti together had 45 marbles, the number of marbles Jivanti had initially = $45 - x$.
After losing 5 marbles each:
Number of marbles John has = $x - 5$.
Number of marbles Jivanti has = $(45 - x) - 5 = 40 - x$.
According to the problem, the product of the number of marbles they now have is 124.
Therefore, $(x - 5)(40 - x) = 124$.
Expanding the expression:
$x(40 - x) - 5(40 - x) = 124$
$40x - x^2 - 200 + 5x = 124$
Combining like terms:
$-x^2 + (40x + 5x) - 200 = 124$
$-x^2 + 45x - 200 = 124$
Bringing all terms to one side:
$-x^2 + 45x - 200 - 124 = 0$
$-x^2 + 45x - 324 = 0$
Multiplying the entire equation by -1 to make the coefficient of $x^2$ positive:
$x^2 - 45x + 324 = 0$.
This is the required quadratic equation representing the situation mathematically.
Solution (ii)
To Find: Mathematical representation of the situation.
Solution:
Let the number of toys produced on that day be $x$.
The cost of production of each toy on that day is given as 55 minus the number of toys produced.
So, the cost of production of each toy = $\textsf{₹} (55 - x)$.
The total cost of production is the product of the number of toys produced and the cost of production of each toy.
Total cost of production = (Number of toys produced) $\times$ (Cost of production of each toy)
Total Cost = $x \times (55 - x)$.
It is given that the total cost of production on that particular day was $\textsf{₹} 750$.
Therefore, $x(55 - x) = 750$.
Expanding the expression:
$55x - x^2 = 750$.
Bringing all terms to one side:
$-x^2 + 55x - 750 = 0$.
Multiplying the entire equation by -1 to make the coefficient of $x^2$ positive:
$x^2 - 55x + 750 = 0$.
This is the required quadratic equation representing the situation mathematically.
Example 2. Check whether the following are quadratic equations:
(i) (x – 2)2 + 1 = 2x – 3
(ii) x(x + 1) + 8 = (x + 2) (x – 2)
(iii) x (2x + 3) = x2 + 1
(iv) (x + 2)3 = x3 – 4
Answer:
General Concept:
A polynomial equation of degree 2 is called a quadratic equation. The standard form of a quadratic equation is $ax^2 + bx + c = 0$, where $a, b, c$ are real numbers and $a \neq 0$.
To check if a given equation is quadratic, we simplify it and see if it can be written in the standard form $ax^2 + bx + c = 0$ with $a \neq 0$.
Solution (i)
Given equation: $(x – 2)^2 + 1 = 2x – 3$
To Check: Whether the given equation is a quadratic equation.
Solution:
We have the equation $(x – 2)^2 + 1 = 2x – 3$.
Expand the term $(x - 2)^2$ using the identity $(a-b)^2 = a^2 - 2ab + b^2$.
$(x^2 - 2(x)(2) + 2^2) + 1 = 2x - 3$
$(x^2 - 4x + 4) + 1 = 2x - 3$
$x^2 - 4x + 5 = 2x - 3$
Now, move all terms to the left-hand side (LHS):
$x^2 - 4x + 5 - 2x + 3 = 0$
Combine like terms:
$x^2 + (-4x - 2x) + (5 + 3) = 0$
$x^2 - 6x + 8 = 0$
This equation is in the form $ax^2 + bx + c = 0$, where $a = 1$, $b = -6$, and $c = 8$.
Since $a = 1 \neq 0$, the degree of the polynomial is 2.
Conclusion: Therefore, the given equation $(x – 2)^2 + 1 = 2x – 3$ is a quadratic equation.
Solution (ii)
Given equation: $x(x + 1) + 8 = (x + 2)(x – 2)$
To Check: Whether the given equation is a quadratic equation.
Solution:
We have the equation $x(x + 1) + 8 = (x + 2)(x – 2)$.
Expand the LHS: $x^2 + x + 8$.
Expand the RHS using the identity $(a+b)(a-b) = a^2 - b^2$.
RHS = $x^2 - 2^2 = x^2 - 4$.
So the equation becomes: $x^2 + x + 8 = x^2 - 4$.
Now, move all terms to the LHS:
$x^2 + x + 8 - x^2 + 4 = 0$
Combine like terms:
$(x^2 - x^2) + x + (8 + 4) = 0$
$0x^2 + x + 12 = 0$
$x + 12 = 0$
This equation is in the form $ax + b = 0$, where $a = 1$ and $b = 12$. The degree of the polynomial is 1.
It cannot be written in the form $ax^2 + bx + c = 0$ with $a \neq 0$ (here $a=0$).
Conclusion: Therefore, the given equation $x(x + 1) + 8 = (x + 2)(x – 2)$ is not a quadratic equation. It is a linear equation.
Solution (iii)
Given equation: $x(2x + 3) = x^2 + 1$
To Check: Whether the given equation is a quadratic equation.
Solution:
We have the equation $x(2x + 3) = x^2 + 1$.
Expand the LHS:
$2x^2 + 3x = x^2 + 1$.
Now, move all terms to the LHS:
$2x^2 + 3x - x^2 - 1 = 0$
Combine like terms:
$(2x^2 - x^2) + 3x - 1 = 0$
$x^2 + 3x - 1 = 0$
This equation is in the form $ax^2 + bx + c = 0$, where $a = 1$, $b = 3$, and $c = -1$.
Since $a = 1 \neq 0$, the degree of the polynomial is 2.
Conclusion: Therefore, the given equation $x(2x + 3) = x^2 + 1$ is a quadratic equation.
Solution (iv)
Given equation: $(x + 2)^3 = x^3 – 4$
To Check: Whether the given equation is a quadratic equation.
Solution:
We have the equation $(x + 2)^3 = x^3 – 4$.
Expand the term $(x + 2)^3$ using the identity $(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$.
$x^3 + 3(x^2)(2) + 3(x)(2^2) + 2^3 = x^3 - 4$
$x^3 + 6x^2 + 3x(4) + 8 = x^3 - 4$
$x^3 + 6x^2 + 12x + 8 = x^3 - 4$
Now, move all terms to the LHS:
$x^3 + 6x^2 + 12x + 8 - x^3 + 4 = 0$
Combine like terms:
$(x^3 - x^3) + 6x^2 + 12x + (8 + 4) = 0$
$0x^3 + 6x^2 + 12x + 12 = 0$
$6x^2 + 12x + 12 = 0$
We can divide the entire equation by 6:
$x^2 + 2x + 2 = 0$
This equation is in the form $ax^2 + bx + c = 0$, where $a = 1$, $b = 2$, and $c = 2$.
Since $a = 1 \neq 0$, the degree of the polynomial is 2.
Conclusion: Therefore, the given equation $(x + 2)^3 = x^3 – 4$ is a quadratic equation.
Exercise 4.1
Question 1. Check whether the following are quadratic equations :
(i) (x + 1)2 = 2(x – 3)
(ii) x2 – 2x = (–2) (3 – x)
(iii) (x – 2)(x + 1) = (x – 1)(x + 3)
(iv) (x – 3)(2x +1) = x(x + 5)
(v) (2x – 1)(x – 3) = (x + 5)(x – 1)
(vi) x2 + 3x + 1 = (x – 2)2
(vii) (x + 2)3 = 2x (x2 – 1)
(viii) x3 – 4x2 – x + 1 = (x – 2)3
Answer:
General Concept:
A polynomial equation of degree 2 is called a quadratic equation. The standard form of a quadratic equation is $ax^2 + bx + c = 0$, where $a, b, c$ are real numbers and $a \neq 0$.
To check if a given equation is quadratic, we simplify it and see if it can be written in the standard form $ax^2 + bx + c = 0$ with $a \neq 0$.
Solution (i)
Given equation: $(x + 1)^2 = 2(x – 3)$
To Check: Whether the given equation is a quadratic equation.
Solution:
We have $(x + 1)^2 = 2(x – 3)$.
Expand the LHS using $(a+b)^2 = a^2 + 2ab + b^2$:
$x^2 + 2(x)(1) + 1^2 = 2(x - 3)$
$x^2 + 2x + 1 = 2x - 6$
Move all terms to the LHS:
$x^2 + 2x + 1 - 2x + 6 = 0$
Combine like terms:
$x^2 + (2x - 2x) + (1 + 6) = 0$
$x^2 + 0x + 7 = 0$
$x^2 + 7 = 0$
This equation is in the form $ax^2 + bx + c = 0$, where $a = 1$, $b = 0$, and $c = 7$.
Since $a = 1 \neq 0$, the degree of the polynomial is 2.
Conclusion: Therefore, the given equation $(x + 1)^2 = 2(x – 3)$ is a quadratic equation.
Solution (ii)
Given equation: $x^2 – 2x = (–2) (3 – x)$
To Check: Whether the given equation is a quadratic equation.
Solution:
We have $x^2 – 2x = (–2) (3 – x)$.
Expand the RHS:
$x^2 - 2x = -2(3) + (-2)(-x)$
$x^2 - 2x = -6 + 2x$
Move all terms to the LHS:
$x^2 - 2x + 6 - 2x = 0$
Combine like terms:
$x^2 + (-2x - 2x) + 6 = 0$
$x^2 - 4x + 6 = 0$
This equation is in the form $ax^2 + bx + c = 0$, where $a = 1$, $b = -4$, and $c = 6$.
Since $a = 1 \neq 0$, the degree of the polynomial is 2.
Conclusion: Therefore, the given equation $x^2 – 2x = (–2) (3 – x)$ is a quadratic equation.
Solution (iii)
Given equation: $(x – 2)(x + 1) = (x – 1)(x + 3)$
To Check: Whether the given equation is a quadratic equation.
Solution:
We have $(x – 2)(x + 1) = (x – 1)(x + 3)$.
Expand both sides:
LHS: $x(x+1) - 2(x+1) = x^2 + x - 2x - 2 = x^2 - x - 2$
RHS: $x(x+3) - 1(x+3) = x^2 + 3x - x - 3 = x^2 + 2x - 3$
So the equation is: $x^2 - x - 2 = x^2 + 2x - 3$.
Move all terms to the LHS:
$x^2 - x - 2 - x^2 - 2x + 3 = 0$
Combine like terms:
$(x^2 - x^2) + (-x - 2x) + (-2 + 3) = 0$
$0x^2 - 3x + 1 = 0$
$-3x + 1 = 0$
This equation is a linear equation ($ax + b = 0$ with $a=-3, b=1$). The highest power of x is 1.
It cannot be written in the form $ax^2 + bx + c = 0$ with $a \neq 0$ (here $a=0$).
Conclusion: Therefore, the given equation $(x – 2)(x + 1) = (x – 1)(x + 3)$ is not a quadratic equation.
Solution (iv)
Given equation: $(x – 3)(2x +1) = x(x + 5)$
To Check: Whether the given equation is a quadratic equation.
Solution:
We have $(x – 3)(2x +1) = x(x + 5)$.
Expand both sides:
LHS: $x(2x+1) - 3(2x+1) = 2x^2 + x - 6x - 3 = 2x^2 - 5x - 3$
RHS: $x(x+5) = x^2 + 5x$
So the equation is: $2x^2 - 5x - 3 = x^2 + 5x$.
Move all terms to the LHS:
$2x^2 - 5x - 3 - x^2 - 5x = 0$
Combine like terms:
$(2x^2 - x^2) + (-5x - 5x) - 3 = 0$
$x^2 - 10x - 3 = 0$
This equation is in the form $ax^2 + bx + c = 0$, where $a = 1$, $b = -10$, and $c = -3$.
Since $a = 1 \neq 0$, the degree of the polynomial is 2.
Conclusion: Therefore, the given equation $(x – 3)(2x +1) = x(x + 5)$ is a quadratic equation.
Solution (v)
Given equation: $(2x – 1)(x – 3) = (x + 5)(x – 1)$
To Check: Whether the given equation is a quadratic equation.
Solution:
We have $(2x – 1)(x – 3) = (x + 5)(x – 1)$.
Expand both sides:
LHS: $2x(x-3) - 1(x-3) = 2x^2 - 6x - x + 3 = 2x^2 - 7x + 3$
RHS: $x(x-1) + 5(x-1) = x^2 - x + 5x - 5 = x^2 + 4x - 5$
So the equation is: $2x^2 - 7x + 3 = x^2 + 4x - 5$.
Move all terms to the LHS:
$2x^2 - 7x + 3 - x^2 - 4x + 5 = 0$
Combine like terms:
$(2x^2 - x^2) + (-7x - 4x) + (3 + 5) = 0$
$x^2 - 11x + 8 = 0$
This equation is in the form $ax^2 + bx + c = 0$, where $a = 1$, $b = -11$, and $c = 8$.
Since $a = 1 \neq 0$, the degree of the polynomial is 2.
Conclusion: Therefore, the given equation $(2x – 1)(x – 3) = (x + 5)(x – 1)$ is a quadratic equation.
Solution (vi)
Given equation: $x^2 + 3x + 1 = (x – 2)^2$
To Check: Whether the given equation is a quadratic equation.
Solution:
We have $x^2 + 3x + 1 = (x – 2)^2$.
Expand the RHS using $(a-b)^2 = a^2 - 2ab + b^2$:
$x^2 + 3x + 1 = x^2 - 2(x)(2) + 2^2$
$x^2 + 3x + 1 = x^2 - 4x + 4$
Move all terms to the LHS:
$x^2 + 3x + 1 - x^2 + 4x - 4 = 0$
Combine like terms:
$(x^2 - x^2) + (3x + 4x) + (1 - 4) = 0$
$0x^2 + 7x - 3 = 0$
$7x - 3 = 0$
This equation is a linear equation ($ax + b = 0$ with $a=7, b=-3$). The highest power of x is 1.
It cannot be written in the form $ax^2 + bx + c = 0$ with $a \neq 0$ (here $a=0$).
Conclusion: Therefore, the given equation $x^2 + 3x + 1 = (x – 2)^2$ is not a quadratic equation.
Solution (vii)
Given equation: $(x + 2)^3 = 2x (x^2 – 1)$
To Check: Whether the given equation is a quadratic equation.
Solution:
We have $(x + 2)^3 = 2x (x^2 – 1)$.
Expand the LHS using $(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$:
$x^3 + 3(x^2)(2) + 3(x)(2^2) + 2^3 = 2x(x^2 - 1)$
$x^3 + 6x^2 + 3x(4) + 8 = 2x^3 - 2x$
$x^3 + 6x^2 + 12x + 8 = 2x^3 - 2x$
Move all terms to the LHS:
$x^3 + 6x^2 + 12x + 8 - 2x^3 + 2x = 0$
Combine like terms:
$(x^3 - 2x^3) + 6x^2 + (12x + 2x) + 8 = 0$
$-x^3 + 6x^2 + 14x + 8 = 0$
Multiply by -1 (optional, for standard form):
$x^3 - 6x^2 - 14x - 8 = 0$
The highest power of x in this equation is 3. Therefore, it is a cubic equation.
Conclusion: Therefore, the given equation $(x + 2)^3 = 2x (x^2 – 1)$ is not a quadratic equation. It is a cubic equation.
Solution (viii)
Given equation: $x^3 – 4x^2 – x + 1 = (x – 2)^3$
To Check: Whether the given equation is a quadratic equation.
Solution:
We have $x^3 – 4x^2 – x + 1 = (x – 2)^3$.
Expand the RHS using $(a-b)^3 = a^3 - 3a^2b + 3ab^2 - b^3$:
$x^3 - 4x^2 - x + 1 = x^3 - 3(x^2)(2) + 3(x)(2^2) - 2^3$
$x^3 - 4x^2 - x + 1 = x^3 - 6x^2 + 3x(4) - 8$
$x^3 - 4x^2 - x + 1 = x^3 - 6x^2 + 12x - 8$
Move all terms from RHS to LHS (or notice the $x^3$ terms cancel):
$x^3 - 4x^2 - x + 1 - x^3 + 6x^2 - 12x + 8 = 0$
Combine like terms:
$(x^3 - x^3) + (-4x^2 + 6x^2) + (-x - 12x) + (1 + 8) = 0$
$0x^3 + 2x^2 - 13x + 9 = 0$
$2x^2 - 13x + 9 = 0$
This equation is in the form $ax^2 + bx + c = 0$, where $a = 2$, $b = -13$, and $c = 9$.
Since $a = 2 \neq 0$, the degree of the polynomial is 2.
Conclusion: Therefore, the given equation $x^3 – 4x^2 – x + 1 = (x – 2)^3$ is a quadratic equation.
Question 2. Represent the following situations in the form of quadratic equations :
(i) The area of a rectangular plot is 528 m2 . The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.
(ii) The product of two consecutive positive integers is 306. We need to find the integers.
(iii) Rohan’s mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find Rohan’s present age.
(iv) A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
Answer:
Solution (i)
Given:
Area of the rectangular plot = 528 m2.
The length of the plot (in metres) is one more than twice its breadth.
To Find:
Represent the situation in the form of a quadratic equation.
Solution:
Let the breadth of the rectangular plot be $x$ metres.
According to the condition, the length of the plot is one more than twice its breadth.
Length = $2 \times (\text{breadth}) + 1 = (2x + 1)$ metres.
We know that the area of a rectangle = Length $\times$ Breadth.
Given Area = 528 m2.
Therefore, $(2x + 1) \times x = 528$.
$2x^2 + x = 528$.
Subtracting 528 from both sides to get the standard quadratic form:
$2x^2 + x - 528 = 0$.
This is the required quadratic equation representing the situation. Here, $x$ represents the breadth of the plot in metres. Since breadth must be positive, $x > 0$.
Solution (ii)
Given:
The product of two consecutive positive integers is 306.
To Find:
Represent the situation in the form of a quadratic equation.
Solution:
Let the first positive integer be $x$.
Since the integers are consecutive, the next positive integer will be $x + 1$.
According to the condition, the product of these two integers is 306.
Therefore, $x \times (x + 1) = 306$.
Expanding the equation:
$x^2 + x = 306$.
Subtracting 306 from both sides to get the standard quadratic form:
$x^2 + x - 306 = 0$.
This is the required quadratic equation representing the situation. Here, $x$ represents the smaller of the two consecutive positive integers, so $x$ must be a positive integer.
Solution (iii)
Given:
Rohan’s mother is 26 years older than him.
The product of their ages (in years) 3 years from now will be 360.
To Find:
Represent the situation in the form of a quadratic equation to find Rohan's present age.
Solution:
Let Rohan's present age be $x$ years.
Since his mother is 26 years older, her present age is $(x + 26)$ years.
Ages 3 years from now:
Rohan's age = $(x + 3)$ years.
Mother's age = $(x + 26) + 3 = (x + 29)$ years.
According to the condition, the product of their ages 3 years from now will be 360.
Therefore, $(x + 3)(x + 29) = 360$.
Expanding the equation:
$x(x + 29) + 3(x + 29) = 360$
$x^2 + 29x + 3x + 87 = 360$
$x^2 + 32x + 87 = 360$
Subtracting 360 from both sides to get the standard quadratic form:
$x^2 + 32x + 87 - 360 = 0$
$x^2 + 32x - 273 = 0$.
This is the required quadratic equation representing the situation. Here, $x$ represents Rohan's present age in years, and $x > 0$.
Solution (iv)
Given:
Distance travelled by the train = 480 km.
The train travels at a uniform speed.
If the speed had been 8 km/h less, it would have taken 3 hours more to cover the same distance.
To Find:
Represent the situation in the form of a quadratic equation to find the speed of the train.
Solution:
Let the uniform speed of the train be $x$ km/h.
We know that Time = $\frac{\text{Distance}}{\text{Speed}}$.
Original time taken to cover 480 km ($T_1$) = $\frac{480}{x}$ hours.
If the speed had been 8 km/h less, the new speed would be $(x - 8)$ km/h.
Time taken to cover 480 km with the new speed ($T_2$) = $\frac{480}{x - 8}$ hours.
According to the condition, the new time ($T_2$) is 3 hours more than the original time ($T_1$).
$T_2 = T_1 + 3$
$\frac{480}{x - 8} = \frac{480}{x} + 3$
Rearranging the terms:
$\frac{480}{x - 8} - \frac{480}{x} = 3$
Taking 480 common from the LHS:
$480 \left( \frac{1}{x - 8} - \frac{1}{x} \right) = 3$
Finding a common denominator inside the parenthesis:
$480 \left( \frac{x - (x - 8)}{x(x - 8)} \right) = 3$
$480 \left( \frac{x - x + 8}{x^2 - 8x} \right) = 3$
$480 \left( \frac{8}{x^2 - 8x} \right) = 3$
$\frac{480 \times 8}{x^2 - 8x} = 3$
$\frac{3840}{x^2 - 8x} = 3$
Cross-multiplying (or multiplying both sides by $x^2 - 8x$):
$3840 = 3(x^2 - 8x)$
Divide both sides by 3:
$1280 = x^2 - 8x$
Rearranging to get the standard quadratic form:
$x^2 - 8x - 1280 = 0$.
This is the required quadratic equation representing the situation. Here, $x$ represents the uniform speed of the train in km/h. Since speed must be positive and the reduced speed $(x-8)$ must also be positive, we have the condition $x > 8$.
Example 3 to 6 (Before Exercise 4.2)
Example 3. Find the roots of the equation 2x2 – 5x + 3 = 0, by factorisation.
Answer:
Given:
The quadratic equation is $2x^2 - 5x + 3 = 0$.
To Find:
The roots of the given equation by the factorisation method.
Solution:
The given quadratic equation is $2x^2 - 5x + 3 = 0$.
To factorise the quadratic expression $ax^2 + bx + c$, we need to find two numbers whose product is $a \times c$ and whose sum is $b$.
In this equation, $a = 2$, $b = -5$, and $c = 3$.
We need two numbers whose product is $a \times c = 2 \times 3 = 6$ and whose sum is $b = -5$.
Let's find pairs of factors of 6:
- 1 and 6 (Sum = 1 + 6 = 7)
- -1 and -6 (Sum = -1 + (-6) = -7)
- 2 and 3 (Sum = 2 + 3 = 5)
- -2 and -3 (Sum = -2 + (-3) = -5)
The pair of numbers that satisfies both conditions (product = 6, sum = -5) is -2 and -3.
Now, we split the middle term ($-5x$) using these two numbers:
$2x^2 - 5x + 3 = 2x^2 - 2x - 3x + 3 = 0$
Next, we factor by grouping the terms:
Group the first two terms and the last two terms:
$(2x^2 - 2x) + (-3x + 3) = 0$
Factor out the greatest common factor (GCF) from each group:
$2x(x - 1) - 3(x - 1) = 0$
Now, factor out the common binomial factor $(x - 1)$:
$(x - 1)(2x - 3) = 0$
According to the Zero Product Property, if the product of two factors is zero, then at least one of the factors must be zero.
So, either $x - 1 = 0$ or $2x - 3 = 0$.
Case 1: $x - 1 = 0$
$x = 1$
Case 2: $2x - 3 = 0$
$2x = 3$
$x = \frac{3}{2}$
Thus, the roots of the equation $2x^2 - 5x + 3 = 0$ are $1$ and $\frac{3}{2}$.
Final Answer:
The roots of the equation $2x^2 - 5x + 3 = 0$ are $\mathbf{1}$ and $\mathbf{\frac{3}{2}}$.
Example 4. Find the roots of the quadratic equation 6x 2 – x – 2 = 0.
Answer:
Given:
The quadratic equation is $6x^2 - x - 2 = 0$.
To Find:
The roots of the given equation.
Solution:
We will find the roots using the factorisation method.
The given quadratic equation is $6x^2 - x - 2 = 0$.
To factorise the quadratic expression $ax^2 + bx + c$, we need to find two numbers whose product is $a \times c$ and whose sum is $b$.
In this equation, $a = 6$, $b = -1$, and $c = -2$.
We need two numbers whose product is $a \times c = 6 \times (-2) = -12$ and whose sum is $b = -1$.
Let's find pairs of factors of -12 and their sums:
- 1 and -12 (Sum = 1 + (-12) = -11)
- -1 and 12 (Sum = -1 + 12 = 11)
- 2 and -6 (Sum = 2 + (-6) = -4)
- -2 and 6 (Sum = -2 + 6 = 4)
- 3 and -4 (Sum = 3 + (-4) = -1)
- -3 and 4 (Sum = -3 + 4 = 1)
The pair of numbers that satisfies both conditions (product = -12, sum = -1) is 3 and -4.
Now, we split the middle term ($-x$) using these two numbers:
$6x^2 - x - 2 = 6x^2 + 3x - 4x - 2 = 0$
Next, we factor by grouping the terms:
Group the first two terms and the last two terms:
$(6x^2 + 3x) + (-4x - 2) = 0$
Factor out the greatest common factor (GCF) from each group:
$3x(2x + 1) - 2(2x + 1) = 0$
Now, factor out the common binomial factor $(2x + 1)$:
$(2x + 1)(3x - 2) = 0$
According to the Zero Product Property, if the product of two factors is zero, then at least one of the factors must be zero.
So, either $2x + 1 = 0$ or $3x - 2 = 0$.
Case 1: $2x + 1 = 0$
$2x = -1$
$x = -\frac{1}{2}$
Case 2: $3x - 2 = 0$
$3x = 2$
$x = \frac{2}{3}$
Thus, the roots of the equation $6x^2 - x - 2 = 0$ are $-\frac{1}{2}$ and $\frac{2}{3}$.
Final Answer:
The roots of the equation $6x^2 - x - 2 = 0$ are $\mathbf{-\frac{1}{2}}$ and $\mathbf{\frac{2}{3}}$.
Example 5. Find the roots of the quadratic equation 3x2 - 2$\sqrt{6}$ x + 2 = 0
Answer:
Given:
The quadratic equation is $3x^2 - 2\sqrt{6}x + 2 = 0$.
To Find:
The roots of the given equation.
Solution:
We will find the roots using the factorisation method.
The given quadratic equation is $3x^2 - 2\sqrt{6}x + 2 = 0$.
To factorise the quadratic expression $ax^2 + bx + c$, we need to find two numbers whose product is $a \times c$ and whose sum is $b$.
In this equation, $a = 3$, $b = -2\sqrt{6}$, and $c = 2$.
We need two numbers whose product is $a \times c = 3 \times 2 = 6$ and whose sum is $b = -2\sqrt{6}$.
Let's consider splitting the middle term coefficient, $-2\sqrt{6}$. We are looking for two numbers $p$ and $q$ such that $p+q = -2\sqrt{6}$ and $p \times q = 6$.
The numbers are $-\sqrt{6}$ and $-\sqrt{6}$.
Check:
Sum: $(-\sqrt{6}) + (-\sqrt{6}) = -2\sqrt{6}$ (Matches $b$)
Product: $(-\sqrt{6}) \times (-\sqrt{6}) = 6$ (Matches $ac$)
Now, we split the middle term ($-2\sqrt{6}x$) using these two numbers:
$3x^2 - \sqrt{6}x - \sqrt{6}x + 2 = 0$
Next, we factor by grouping the terms. We can rewrite the coefficients to make factoring easier:
Note that $3 = (\sqrt{3})^2$, $\sqrt{6} = \sqrt{3} \times \sqrt{2}$, and $2 = (\sqrt{2})^2$.
So the equation becomes: $(\sqrt{3})^2 x^2 - (\sqrt{3}\sqrt{2})x - (\sqrt{3}\sqrt{2})x + (\sqrt{2})^2 = 0$
Group the first two terms and the last two terms:
$[(\sqrt{3})^2 x^2 - (\sqrt{3}\sqrt{2})x] + [-(\sqrt{3}\sqrt{2})x + (\sqrt{2})^2] = 0$
Factor out the greatest common factor (GCF) from each group:
From the first group, the GCF is $\sqrt{3}x$:
$\sqrt{3}x (\sqrt{3}x - \sqrt{2})$
From the second group, the GCF is $-\sqrt{2}$ (factoring out the negative sign):
$-\sqrt{2} (\sqrt{3}x - \sqrt{2})$
Substitute back into the equation:
$\sqrt{3}x (\sqrt{3}x - \sqrt{2}) - \sqrt{2} (\sqrt{3}x - \sqrt{2}) = 0$
Now, factor out the common binomial factor $(\sqrt{3}x - \sqrt{2})$:
$(\sqrt{3}x - \sqrt{2})(\sqrt{3}x - \sqrt{2}) = 0$
This can be written as $(\sqrt{3}x - \sqrt{2})^2 = 0$.
According to the Zero Product Property, we set the factor equal to zero:
$\sqrt{3}x - \sqrt{2} = 0$
$\sqrt{3}x = \sqrt{2}$
$x = \frac{\sqrt{2}}{\sqrt{3}}$
To rationalize the denominator, multiply the numerator and denominator by $\sqrt{3}$:
$x = \frac{\sqrt{2} \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{6}}{3}$
Since the factor $(\sqrt{3}x - \sqrt{2})$ is repeated, the quadratic equation has two equal real roots.
Thus, the roots of the equation $3x^2 - 2\sqrt{6}x + 2 = 0$ are $\frac{\sqrt{6}}{3}$ and $\frac{\sqrt{6}}{3}$.
Final Answer:
The roots of the equation $3x^2 - 2\sqrt{6}x + 2 = 0$ are $\mathbf{\frac{\sqrt{6}}{3}}$ and $\mathbf{\frac{\sqrt{6}}{3}}$.
Example 6. Find the dimensions of the prayer hall discussed in Section 4.1.
Prayer Hall discussed in Section 4.1: Suppose a charity trust decides to build a prayer hall having a carpet area of 300 square metres with its length one metre more than twice its breadth. What should be the length and breadth of the hall?
Answer:
Given:
A rectangular prayer hall.
Carpet Area = 300 m2.
Length = 1 metre more than twice its breadth.
To Find:
The length and breadth of the prayer hall.
Solution:
Let the breadth of the prayer hall be $x$ metres.
According to the given condition, the length is one metre more than twice its breadth.
Length = $2 \times (\text{breadth}) + 1 = (2x + 1)$ metres.
The area of a rectangle is given by the formula: Area = Length $\times$ Breadth.
We are given that the area is 300 m2.
Therefore, $(2x + 1) \times x = 300$.
Expanding the equation:
$2x^2 + x = 300$.
Rearranging the terms to form a standard quadratic equation:
$2x^2 + x - 300 = 0$.
Now, we need to solve this quadratic equation for $x$. We can use the factorisation method.
We need to find two numbers whose product is $a \times c = 2 \times (-300) = -600$ and whose sum is $b = 1$.
Let's find pairs of factors of -600 whose sum is 1.
Consider the factors 25 and -24:
Product = $25 \times (-24) = -600$.
Sum = $25 + (-24) = 1$.
These numbers satisfy the conditions.
Now, split the middle term ($x$) using these numbers:
$2x^2 + 25x - 24x - 300 = 0$.
Factor by grouping:
$(2x^2 + 25x) + (-24x - 300) = 0$.
Factor out the GCF from each group:
$x(2x + 25) - 12(2x + 25) = 0$.
Factor out the common binomial factor $(2x + 25)$:
$(2x + 25)(x - 12) = 0$.
Using the Zero Product Property, set each factor to zero:
Either $2x + 25 = 0$ or $x - 12 = 0$.
Case 1: $2x + 25 = 0$
$2x = -25$
$x = -\frac{25}{2} = -12.5$.
Case 2: $x - 12 = 0$
$x = 12$.
Since $x$ represents the breadth of the hall, it must be a positive value. Therefore, $x = -12.5$ is not a valid solution.
The breadth of the hall is $x = 12$ metres.
Now, calculate the length using the expression Length = $2x + 1$:
Length = $2(12) + 1 = 24 + 1 = 25$ metres.
Final Answer:
The dimensions of the prayer hall are:
Breadth = 12 metres
Length = 25 metres
(Check: Area = $12 \times 25 = 300$ m2. Length $25 = 2 \times 12 + 1$. Conditions are satisfied.)
Exercise 4.2
Question 1. Find the roots of the following quadratic equations by factorisation:
(i) x2 – 3x – 10 = 0
(ii) 2x2 + x – 6 = 0
(iii) $\sqrt{2}$ x2 + 7x + 5$\sqrt{2}$ = 0
(iv) 2x2 - x + $\frac{1}{8}$ = 0
(v) 100x2 - 20x + 1 = 0
Answer:
Solution (i)
Given equation: $x^2 – 3x – 10 = 0$
To Find: Roots by factorisation.
Solution:
We need to find two numbers whose product is $1 \times (-10) = -10$ and whose sum is $-3$.
The pairs of factors of -10 are (1, -10), (-1, 10), (2, -5), (-2, 5).
The pair whose sum is -3 is 2 and -5.
Splitting the middle term:
$x^2 + 2x - 5x - 10 = 0$
Grouping the terms:
$(x^2 + 2x) + (-5x - 10) = 0$
Factoring out the GCF from each group:
$x(x + 2) - 5(x + 2) = 0$
Factoring out the common binomial factor $(x + 2)$:
$(x + 2)(x - 5) = 0$
By the Zero Product Property:
Either $x + 2 = 0 \implies x = -2$
Or $x - 5 = 0 \implies x = 5$
Conclusion: The roots of the equation $x^2 – 3x – 10 = 0$ are $\mathbf{-2}$ and $\mathbf{5}$.
Solution (ii)
Given equation: $2x^2 + x – 6 = 0$
To Find: Roots by factorisation.
Solution:
We need to find two numbers whose product is $2 \times (-6) = -12$ and whose sum is $1$.
The pairs of factors of -12 are (1, -12), (-1, 12), (2, -6), (-2, 6), (3, -4), (-3, 4).
The pair whose sum is 1 is -3 and 4.
Splitting the middle term:
$2x^2 - 3x + 4x - 6 = 0$
Grouping the terms:
$(2x^2 - 3x) + (4x - 6) = 0$
Factoring out the GCF from each group:
$x(2x - 3) + 2(2x - 3) = 0$
Factoring out the common binomial factor $(2x - 3)$:
$(2x - 3)(x + 2) = 0$
By the Zero Product Property:
Either $2x - 3 = 0 \implies 2x = 3 \implies x = \frac{3}{2}$
Or $x + 2 = 0 \implies x = -2$
Conclusion: The roots of the equation $2x^2 + x – 6 = 0$ are $\mathbf{-2}$ and $\mathbf{\frac{3}{2}}$.
Solution (iii)
Given equation: $\sqrt{2}x^2 + 7x + 5\sqrt{2} = 0$
To Find: Roots by factorisation.
Solution:
We need to find two numbers whose product is $\sqrt{2} \times 5\sqrt{2} = 5 \times (\sqrt{2})^2 = 5 \times 2 = 10$ and whose sum is $7$.
The pairs of factors of 10 are (1, 10), (-1, -10), (2, 5), (-2, -5).
The pair whose sum is 7 is 2 and 5.
Splitting the middle term:
$\sqrt{2}x^2 + 2x + 5x + 5\sqrt{2} = 0$
Grouping the terms. Note that $2 = \sqrt{2} \times \sqrt{2}$.
$(\sqrt{2}x^2 + \sqrt{2}\sqrt{2}x) + (5x + 5\sqrt{2}) = 0$
Factoring out the GCF from each group:
$\sqrt{2}x(x + \sqrt{2}) + 5(x + \sqrt{2}) = 0$
Factoring out the common binomial factor $(x + \sqrt{2})$:
$(x + \sqrt{2})(\sqrt{2}x + 5) = 0$
By the Zero Product Property:
Either $x + \sqrt{2} = 0 \implies x = -\sqrt{2}$
Or $\sqrt{2}x + 5 = 0 \implies \sqrt{2}x = -5 \implies x = -\frac{5}{\sqrt{2}}$
Rationalizing the denominator for the second root: $x = -\frac{5}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = -\frac{5\sqrt{2}}{2}$
Conclusion: The roots of the equation $\sqrt{2}x^2 + 7x + 5\sqrt{2} = 0$ are $\mathbf{-\sqrt{2}}$ and $\mathbf{-\frac{5\sqrt{2}}{2}}$.
Solution (iv)
Given equation: $2x^2 - x + \frac{1}{8} = 0$
To Find: Roots by factorisation.
Solution:
First, multiply the entire equation by 8 to eliminate the fraction:
$8 \times (2x^2 - x + \frac{1}{8}) = 8 \times 0$
$16x^2 - 8x + 1 = 0$
Now, factorise $16x^2 - 8x + 1 = 0$. We need two numbers whose product is $16 \times 1 = 16$ and whose sum is $-8$.
The pair of numbers is -4 and -4.
Splitting the middle term:
$16x^2 - 4x - 4x + 1 = 0$
Grouping the terms:
$(16x^2 - 4x) + (-4x + 1) = 0$
Factoring out the GCF from each group:
$4x(4x - 1) - 1(4x - 1) = 0$
Factoring out the common binomial factor $(4x - 1)$:
$(4x - 1)(4x - 1) = 0$
$(4x - 1)^2 = 0$
By the Zero Product Property:
$4x - 1 = 0 \implies 4x = 1 \implies x = \frac{1}{4}$
Since the factor is repeated, we have equal roots.
Conclusion: The roots of the equation $2x^2 - x + \frac{1}{8} = 0$ are $\mathbf{\frac{1}{4}}$ and $\mathbf{\frac{1}{4}}$.
Solution (v)
Given equation: $100x^2 - 20x + 1 = 0$
To Find: Roots by factorisation.
Solution:
We need to find two numbers whose product is $100 \times 1 = 100$ and whose sum is $-20$.
The pair of numbers is -10 and -10.
Splitting the middle term:
$100x^2 - 10x - 10x + 1 = 0$
Grouping the terms:
$(100x^2 - 10x) + (-10x + 1) = 0$
Factoring out the GCF from each group:
$10x(10x - 1) - 1(10x - 1) = 0$
Factoring out the common binomial factor $(10x - 1)$:
$(10x - 1)(10x - 1) = 0$
$(10x - 1)^2 = 0$
By the Zero Product Property:
$10x - 1 = 0 \implies 10x = 1 \implies x = \frac{1}{10}$
Since the factor is repeated, we have equal roots.
Conclusion: The roots of the equation $100x^2 - 20x + 1 = 0$ are $\mathbf{\frac{1}{10}}$ and $\mathbf{\frac{1}{10}}$.
Question 2. Solve the problems given in Example 1.
Problems in Example 1.
(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 124. We would like to find out how many marbles they had to start with.
(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was ₹ 750. We would like to find out the number of toys produced on that day.
Answer:
Solution (i)
From Example 1(i), the mathematical representation of the situation is the quadratic equation:
$x^2 - 45x + 324 = 0$
where $x$ is the number of marbles John had initially.
To Find: The initial number of marbles John and Jivanti had.
Solution:
We solve the quadratic equation $x^2 - 45x + 324 = 0$ by factorisation.
We need two numbers whose product is $1 \times 324 = 324$ and whose sum is $-45$.
Since the product is positive and the sum is negative, both numbers must be negative.
Let's find factors of 324. We find that $36 \times 9 = 324$ and $36 + 9 = 45$.
So, the two numbers are $-36$ and $-9$.
Splitting the middle term:
$x^2 - 9x - 36x + 324 = 0$
Grouping the terms:
$(x^2 - 9x) + (-36x + 324) = 0$
Factoring out the GCF from each group:
$x(x - 9) - 36(x - 9) = 0$
Factoring out the common binomial factor $(x - 9)$:
$(x - 9)(x - 36) = 0$
By the Zero Product Property:
Either $x - 9 = 0 \implies x = 9$
Or $x - 36 = 0 \implies x = 36$
So, the possible number of marbles John had initially is 9 or 36.
Case 1: If John had $x=9$ marbles, then Jivanti had $45 - x = 45 - 9 = 36$ marbles.
Case 2: If John had $x=36$ marbles, then Jivanti had $45 - x = 45 - 36 = 9$ marbles.
In both cases, one person had 9 marbles and the other had 36 marbles initially.
Check: If they had 9 and 36 marbles. After losing 5 each, they have $9-5=4$ and $36-5=31$ marbles. Product = $4 \times 31 = 124$. This matches the given condition.
Conclusion: The number of marbles they had to start with were $\mathbf{9}$ and $\mathbf{36}$.
Solution (ii)
From Example 1(ii), the mathematical representation of the situation is the quadratic equation:
$x^2 - 55x + 750 = 0$
where $x$ is the number of toys produced on that day.
To Find: The number of toys produced on that day.
Solution:
We solve the quadratic equation $x^2 - 55x + 750 = 0$ by factorisation.
We need two numbers whose product is $1 \times 750 = 750$ and whose sum is $-55$.
Since the product is positive and the sum is negative, both numbers must be negative.
Let's find factors of 750. We find that $25 \times 30 = 750$ and $25 + 30 = 55$.
So, the two numbers are $-25$ and $-30$.
Splitting the middle term:
$x^2 - 25x - 30x + 750 = 0$
Grouping the terms:
$(x^2 - 25x) + (-30x + 750) = 0$
Factoring out the GCF from each group:
$x(x - 25) - 30(x - 25) = 0$
Factoring out the common binomial factor $(x - 25)$:
$(x - 25)(x - 30) = 0$
By the Zero Product Property:
Either $x - 25 = 0 \implies x = 25$
Or $x - 30 = 0 \implies x = 30$
Both values are possible numbers for the toys produced.
Case 1: If $x=25$ toys were produced, the cost of each toy is $55 - 25 = \textsf{₹} 30$. Total cost = $25 \times 30 = \textsf{₹} 750$.
Case 2: If $x=30$ toys were produced, the cost of each toy is $55 - 30 = \textsf{₹} 25$. Total cost = $30 \times 25 = \textsf{₹} 750$.
Both scenarios fit the problem description.
Conclusion: The number of toys produced on that day was either $\mathbf{25}$ or $\mathbf{30}$.
Question 3. Find two numbers whose sum is 27 and product is 182.
Answer:
Given:
The sum of two numbers is 27.
The product of the two numbers is 182.
To Find:
The two numbers.
Solution:
Let the two numbers be $x$ and $y$.
According to the problem statement, we have the following equations:
$x + y = 27$
...(i)
$x \times y = 182$
...(ii)
From equation (i), we can express $y$ in terms of $x$:
$y = 27 - x$
Now substitute this expression for $y$ into equation (ii):
$x(27 - x) = 182$
Expand the equation:
$27x - x^2 = 182$
Rearrange the terms to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$-x^2 + 27x - 182 = 0$
Multiply the entire equation by -1 to make the leading coefficient positive:
$x^2 - 27x + 182 = 0$
Now, we solve this quadratic equation by factorisation.
We need to find two numbers whose product is $1 \times 182 = 182$ and whose sum is $-27$.
Since the product is positive and the sum is negative, both numbers must be negative.
Let's find the factors of 182:
$182 = 2 \times 91 = 2 \times 7 \times 13$.
The pairs of factors are (1, 182), (2, 91), (7, 26), (13, 14).
The sum of 13 and 14 is $13 + 14 = 27$. Since we need a sum of -27, the required numbers are -13 and -14.
Split the middle term ($-27x$) using -13 and -14:
$x^2 - 13x - 14x + 182 = 0$
Factor by grouping:
$(x^2 - 13x) + (-14x + 182) = 0$
$x(x - 13) - 14(x - 13) = 0$
Factor out the common binomial factor $(x - 13)$:
$(x - 13)(x - 14) = 0$
Using the Zero Product Property, set each factor equal to zero:
Either $x - 13 = 0 \implies x = 13$
Or $x - 14 = 0 \implies x = 14$
Now, find the corresponding value of $y$ using $y = 27 - x$.
If $x = 13$, then $y = 27 - 13 = 14$.
If $x = 14$, then $y = 27 - 14 = 13$.
In both cases, the two numbers are 13 and 14.
Check:
Sum: $13 + 14 = 27$. (Correct)
Product: $13 \times 14 = 182$. (Correct)
Final Answer:
The two numbers are $\mathbf{13}$ and $\mathbf{14}$.
Question 4. Find two consecutive positive integers, sum of whose squares is 365.
Answer:
Given:
Two consecutive positive integers.
The sum of the squares of these integers is 365.
To Find:
The two consecutive positive integers.
Solution:
Let the first positive integer be $x$.
Since the integers are consecutive, the next positive integer is $x + 1$.
According to the problem statement, the sum of the squares of these two integers is 365.
Square of the first integer = $x^2$.
Square of the second integer = $(x + 1)^2$.
The equation representing the condition is:
$x^2 + (x + 1)^2 = 365$
Expand the term $(x + 1)^2$ using the identity $(a+b)^2 = a^2 + 2ab + b^2$:
$(x + 1)^2 = x^2 + 2(x)(1) + 1^2 = x^2 + 2x + 1$
Substitute this back into the equation:
$x^2 + (x^2 + 2x + 1) = 365$
Combine like terms:
$2x^2 + 2x + 1 = 365$
Subtract 365 from both sides to set the equation to zero:
$2x^2 + 2x + 1 - 365 = 0$
$2x^2 + 2x - 364 = 0$
Divide the entire equation by 2 to simplify:
$\frac{2x^2}{2} + \frac{2x}{2} - \frac{364}{2} = \frac{0}{2}$
$x^2 + x - 182 = 0$
Now, we solve this quadratic equation by factorisation.
We need to find two numbers whose product is $1 \times (-182) = -182$ and whose sum is $1$.
Let's find the factors of 182: $182 = 2 \times 91 = 2 \times 7 \times 13$.
We look for two factors whose difference is 1. These are 13 and 14.
Since the sum is positive (+1), the larger factor (14) must be positive, and the smaller factor (13) must be negative. The two numbers are 14 and -13.
Check: Product = $14 \times (-13) = -182$. Sum = $14 + (-13) = 1$.
Split the middle term ($x$) using 14 and -13:
$x^2 + 14x - 13x - 182 = 0$
Factor by grouping:
$(x^2 + 14x) + (-13x - 182) = 0$
$x(x + 14) - 13(x + 14) = 0$
Factor out the common binomial factor $(x + 14)$:
$(x + 14)(x - 13) = 0$
Using the Zero Product Property, set each factor equal to zero:
Either $x + 14 = 0 \implies x = -14$
Or $x - 13 = 0 \implies x = 13$
The problem asks for positive integers. Therefore, $x = -14$ is not a valid solution.
The first positive integer is $x = 13$.
The second consecutive positive integer is $x + 1 = 13 + 1 = 14$.
Check:
The integers are 13 and 14. They are consecutive and positive.
Sum of their squares = $13^2 + 14^2 = 169 + 196 = 365$. (Correct)
Final Answer:
The two consecutive positive integers are $\mathbf{13}$ and $\mathbf{14}$.
Question 5. The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Answer:
Given:
A right-angled triangle.
The altitude is 7 cm less than its base.
The hypotenuse is 13 cm.
To Find:
The lengths of the other two sides (base and altitude).
Solution:
Let the base of the right triangle be $x$ cm.
According to the problem statement, the altitude is 7 cm less than the base.
So, Altitude = $(x - 7)$ cm.
The hypotenuse is given as 13 cm.
By the Pythagorean theorem, for a right-angled triangle:
$(\text{Base})^2 + (\text{Altitude})^2 = (\text{Hypotenuse})^2$
Substituting the values:
$x^2 + (x - 7)^2 = 13^2$
Expand $(x - 7)^2$ using the identity $(a-b)^2 = a^2 - 2ab + b^2$:
$(x - 7)^2 = x^2 - 2(x)(7) + 7^2 = x^2 - 14x + 49$
Substitute this back into the Pythagorean equation:
$x^2 + (x^2 - 14x + 49) = 169$
Combine like terms:
$2x^2 - 14x + 49 = 169$
Move all terms to one side to form a quadratic equation:
$2x^2 - 14x + 49 - 169 = 0$
$2x^2 - 14x - 120 = 0$
Divide the entire equation by 2 to simplify:
$\frac{2x^2}{2} - \frac{14x}{2} - \frac{120}{2} = \frac{0}{2}$
$x^2 - 7x - 60 = 0$
Now, solve this quadratic equation by factorisation.
We need to find two numbers whose product is $1 \times (-60) = -60$ and whose sum is $-7$.
The factors of -60 whose sum is -7 are 5 and -12. ($5 \times -12 = -60$ and $5 + (-12) = -7$)
Split the middle term ($-7x$):
$x^2 + 5x - 12x - 60 = 0$
Factor by grouping:
$(x^2 + 5x) + (-12x - 60) = 0$
$x(x + 5) - 12(x + 5) = 0$
Factor out the common binomial factor $(x + 5)$:
$(x + 5)(x - 12) = 0$
Using the Zero Product Property, set each factor equal to zero:
Either $x + 5 = 0 \implies x = -5$
Or $x - 12 = 0 \implies x = 12$
Since $x$ represents the length of the base of the triangle, it cannot be negative. Therefore, $x = -5$ is rejected.
The base of the triangle is $x = 12$ cm.
The altitude of the triangle is $x - 7 = 12 - 7 = 5$ cm.
Check:
Base = 12 cm, Altitude = 5 cm, Hypotenuse = 13 cm.
Altitude (5 cm) is 7 cm less than Base (12 cm). (Correct)
Check Pythagorean theorem: $12^2 + 5^2 = 144 + 25 = 169$. And $13^2 = 169$. The theorem holds true.
Final Answer:
The other two sides of the right triangle are its base = 12 cm and its altitude = 5 cm.
Question 6. A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was ₹ 90, find the number of articles produced and the cost of each article.
Answer:
Given:
A cottage industry produces pottery articles.
Cost of production of each article = 3 more than twice the number of articles produced that day.
Total cost of production on that day = $\textsf{₹} 90$.
To Find:
The number of articles produced on that day.
The cost of each article.
Solution:
Let the number of pottery articles produced on that day be $x$.
According to the problem statement, the cost of production of each article (in rupees) was 3 more than twice the number of articles produced.
Cost of each article = $2 \times (\text{Number of articles}) + 3 = (2x + 3)$ rupees.
The total cost of production is the product of the number of articles and the cost of each article.
Total Cost = (Number of articles) $\times$ (Cost of each article)
Given that the total cost of production was $\textsf{₹} 90$.
Therefore, $x \times (2x + 3) = 90$.
Expand the equation:
$2x^2 + 3x = 90$.
Rearrange the terms to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$2x^2 + 3x - 90 = 0$.
Now, we solve this quadratic equation by factorisation.
We need to find two numbers whose product is $a \times c = 2 \times (-90) = -180$ and whose sum is $b = 3$.
Since the product is negative, the two numbers must have opposite signs. Since the sum is positive, the larger number (in magnitude) must be positive.
Factors of 180 are: (1, 180), (2, 90), (3, 60), (4, 45), (5, 36), (6, 30), (9, 20), (10, 18), (12, 15).
We need a pair whose difference is 3. The pair is 12 and 15.
To get a sum of +3, the numbers must be 15 and -12.
Check: Product = $15 \times (-12) = -180$. Sum = $15 + (-12) = 3$.
Split the middle term ($3x$) using 15 and -12:
$2x^2 + 15x - 12x - 90 = 0$.
Factor by grouping:
$(2x^2 + 15x) + (-12x - 90) = 0$.
$x(2x + 15) - 6(2x + 15) = 0$.
Factor out the common binomial factor $(2x + 15)$:
$(2x + 15)(x - 6) = 0$.
Using the Zero Product Property, set each factor equal to zero:
Either $2x + 15 = 0 \implies 2x = -15 \implies x = -\frac{15}{2}$.
Or $x - 6 = 0 \implies x = 6$.
Since $x$ represents the number of articles produced, it must be a positive integer. Therefore, $x = -\frac{15}{2}$ is not a valid solution.
The number of articles produced on that day is $x = 6$.
Now, find the cost of each article using the expression Cost = $2x + 3$:
Cost of each article = $2(6) + 3 = 12 + 3 = 15$ rupees.
Check:
Number of articles = 6.
Cost of each article = $\textsf{₹} 15$.
Total cost = $6 \times 15 = \textsf{₹} 90$. This matches the given information.
Also, the cost ($\textsf{₹} 15$) is 3 more than twice the number of articles ($2 \times 6 + 3 = 12 + 3 = 15$). This condition is also satisfied.
Final Answer:
The number of articles produced on that day is $\mathbf{6}$.
The cost of each article is $\mathbf{\textsf{₹} 15}$.
Example 7 to 15 (Before Exercise 4.3)
Example 7. Solve the equation given in Example 3 by the method of completing the square.
Equation provided in Example 3 - “2x2 – 5x + 3 = 0”
Answer:
Given:
The quadratic equation is $2x^2 - 5x + 3 = 0$.
To Find:
The roots of the given equation by the method of completing the square.
Solution:
The given equation is $2x^2 - 5x + 3 = 0$.
Step 1: Divide the entire equation by the coefficient of $x^2$, which is 2, to make the coefficient of $x^2$ equal to 1.
$\frac{2x^2}{2} - \frac{5x}{2} + \frac{3}{2} = \frac{0}{2}$
$x^2 - \frac{5}{2}x + \frac{3}{2} = 0$
Step 2: Move the constant term ($\frac{3}{2}$) to the right-hand side (RHS).
$x^2 - \frac{5}{2}x = -\frac{3}{2}$
Step 3: Take half of the coefficient of the $x$ term, square it, and add it to both sides.
The coefficient of $x$ is $-\frac{5}{2}$.
Half of the coefficient is $\frac{1}{2} \times (-\frac{5}{2}) = -\frac{5}{4}$.
Squaring this value: $(-\frac{5}{4})^2 = \frac{25}{16}$.
Add $\frac{25}{16}$ to both sides of the equation:
$x^2 - \frac{5}{2}x + \frac{25}{16} = -\frac{3}{2} + \frac{25}{16}$
Step 4: Factor the left-hand side (LHS) as a perfect square.
The LHS is now $(x - \frac{5}{4})^2$.
$(x - \frac{5}{4})^2 = -\frac{3}{2} + \frac{25}{16}$
Step 5: Simplify the RHS.
Find a common denominator for the RHS, which is 16.
$-\frac{3}{2} = -\frac{3 \times 8}{2 \times 8} = -\frac{24}{16}$
$(x - \frac{5}{4})^2 = -\frac{24}{16} + \frac{25}{16}$
$(x - \frac{5}{4})^2 = \frac{-24 + 25}{16}$
$(x - \frac{5}{4})^2 = \frac{1}{16}$
Step 6: Take the square root of both sides.
$x - \frac{5}{4} = \pm \sqrt{\frac{1}{16}}$
$x - \frac{5}{4} = \pm \frac{1}{4}$
Step 7: Solve for $x$.
$x = \frac{5}{4} \pm \frac{1}{4}$
We have two possible values for $x$:
Case 1: Using the '+' sign
$x = \frac{5}{4} + \frac{1}{4} = \frac{5+1}{4} = \frac{6}{4} = \frac{3}{2}$
Case 2: Using the '-' sign
$x = \frac{5}{4} - \frac{1}{4} = \frac{5-1}{4} = \frac{4}{4} = 1$
Final Answer:
The roots of the equation $2x^2 - 5x + 3 = 0$, found by completing the square, are $\mathbf{1}$ and $\mathbf{\frac{3}{2}}$.
Example 8. Find the roots of the equation 5x2 – 6x – 2 = 0 by the method of completing the square.
Answer:
Given:
The quadratic equation is $5x^2 - 6x - 2 = 0$.
To Find:
The roots of the given equation by the method of completing the square.
Solution:
The given equation is $5x^2 - 6x - 2 = 0$.
Step 1: Divide the entire equation by the coefficient of $x^2$, which is 5, to make the coefficient of $x^2$ equal to 1.
$\frac{5x^2}{5} - \frac{6x}{5} - \frac{2}{5} = \frac{0}{5}$
$x^2 - \frac{6}{5}x - \frac{2}{5} = 0$
Step 2: Move the constant term ($-\frac{2}{5}$) to the right-hand side (RHS).
$x^2 - \frac{6}{5}x = \frac{2}{5}$
Step 3: Take half of the coefficient of the $x$ term, square it, and add it to both sides.
The coefficient of $x$ is $-\frac{6}{5}$.
Half of the coefficient is $\frac{1}{2} \times (-\frac{6}{5}) = -\frac{3}{5}$.
Squaring this value: $(-\frac{3}{5})^2 = \frac{9}{25}$.
Add $\frac{9}{25}$ to both sides of the equation:
$x^2 - \frac{6}{5}x + \frac{9}{25} = \frac{2}{5} + \frac{9}{25}$
Step 4: Factor the left-hand side (LHS) as a perfect square.
The LHS is now $(x - \frac{3}{5})^2$.
$(x - \frac{3}{5})^2 = \frac{2}{5} + \frac{9}{25}$
Step 5: Simplify the RHS.
Find a common denominator for the RHS, which is 25.
$\frac{2}{5} = \frac{2 \times 5}{5 \times 5} = \frac{10}{25}$
$(x - \frac{3}{5})^2 = \frac{10}{25} + \frac{9}{25}$
$(x - \frac{3}{5})^2 = \frac{10 + 9}{25}$
$(x - \frac{3}{5})^2 = \frac{19}{25}$
Step 6: Take the square root of both sides.
$x - \frac{3}{5} = \pm \sqrt{\frac{19}{25}}$
$x - \frac{3}{5} = \pm \frac{\sqrt{19}}{\sqrt{25}}$
$x - \frac{3}{5} = \pm \frac{\sqrt{19}}{5}$
Step 7: Solve for $x$.
$x = \frac{3}{5} \pm \frac{\sqrt{19}}{5}$
$x = \frac{3 \pm \sqrt{19}}{5}$
The two roots are $x = \frac{3 + \sqrt{19}}{5}$ and $x = \frac{3 - \sqrt{19}}{5}$.
Final Answer:
The roots of the equation $5x^2 - 6x - 2 = 0$, found by completing the square, are $\mathbf{\frac{3 + \sqrt{19}}{5}}$ and $\mathbf{\frac{3 - \sqrt{19}}{5}}$.
Example 9. Find the roots of 4x2 + 3x + 5 = 0 by the method of completing the square.
Answer:
Given:
The quadratic equation is $4x^2 + 3x + 5 = 0$.
To Find:
The roots of the given equation by the method of completing the square.
Solution:
The given equation is $4x^2 + 3x + 5 = 0$.
Step 1: Divide the entire equation by the coefficient of $x^2$, which is 4, to make the coefficient of $x^2$ equal to 1.
$\frac{4x^2}{4} + \frac{3x}{4} + \frac{5}{4} = \frac{0}{4}$
$x^2 + \frac{3}{4}x + \frac{5}{4} = 0$
Step 2: Move the constant term ($\frac{5}{4}$) to the right-hand side (RHS).
$x^2 + \frac{3}{4}x = -\frac{5}{4}$
Step 3: Take half of the coefficient of the $x$ term, square it, and add it to both sides.
The coefficient of $x$ is $\frac{3}{4}$.
Half of the coefficient is $\frac{1}{2} \times \frac{3}{4} = \frac{3}{8}$.
Squaring this value: $(\frac{3}{8})^2 = \frac{9}{64}$.
Add $\frac{9}{64}$ to both sides of the equation:
$x^2 + \frac{3}{4}x + \frac{9}{64} = -\frac{5}{4} + \frac{9}{64}$
Step 4: Factor the left-hand side (LHS) as a perfect square.
The LHS is now $(x + \frac{3}{8})^2$.
$(x + \frac{3}{8})^2 = -\frac{5}{4} + \frac{9}{64}$
Step 5: Simplify the RHS.
Find a common denominator for the RHS, which is 64.
$-\frac{5}{4} = -\frac{5 \times 16}{4 \times 16} = -\frac{80}{64}$
$(x + \frac{3}{8})^2 = -\frac{80}{64} + \frac{9}{64}$
$(x + \frac{3}{8})^2 = \frac{-80 + 9}{64}$
$(x + \frac{3}{8})^2 = -\frac{71}{64}$
Step 6: Analyze the result.
The square of any real number cannot be negative. However, the expression $(x + \frac{3}{8})^2$ is equal to a negative number ($-\frac{71}{64}$).
This means that there is no real value of $x$ that satisfies the equation $(x + \frac{3}{8})^2 = -\frac{71}{64}$.
Therefore, the original quadratic equation $4x^2 + 3x + 5 = 0$ has no real roots.
Final Answer:
The equation $4x^2 + 3x + 5 = 0$ has no real roots because the square of a real number cannot be negative.
Example 10. Solve Q. 2(i) of Exercise 4.1 by using the quadratic formula
“Q.2(i) of Exercise 4.1 - (i) The area of a rectangular plot is 528 m2 . The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.”
Answer:
Given:
A rectangular plot with Area = 528 m2.
Length of the plot = $1 + 2 \times (\text{Breadth})$.
To Find:
The length and breadth of the plot using the quadratic formula.
Solution:
First, let's set up the quadratic equation representing the situation, as derived in Exercise 4.1, Q.2(i).
Let the breadth of the plot be $x$ metres.
Then, the length of the plot is $(2x + 1)$ metres.
Area = Length $\times$ Breadth
$528 = (2x + 1)x$
$528 = 2x^2 + x$
Rearranging into the standard quadratic form $ax^2 + bx + c = 0$:
$2x^2 + x - 528 = 0$
Now, we will solve this equation using the quadratic formula.
Compare the equation $2x^2 + x - 528 = 0$ with the standard form $ax^2 + bx + c = 0$.
We have: $a = 2$, $b = 1$, $c = -528$.
The quadratic formula is given by:
$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
First, calculate the discriminant, $D = b^2 - 4ac$:
$D = (1)^2 - 4(2)(-528)$
$D = 1 - 8(-528)$
$D = 1 + 4224$
$D = 4225$
Since $D > 0$, the equation has two distinct real roots.
Now, substitute the values of $a$, $b$, and the discriminant $D$ into the quadratic formula:
$x = \frac{-(1) \pm \sqrt{4225}}{2(2)}$
We need to find the square root of 4225. We know $60^2 = 3600$ and $70^2 = 4900$. Since it ends in 5, the square root must end in 5. Let's check $65^2 = 4225$.
So, $\sqrt{4225} = 65$.
$x = \frac{-1 \pm 65}{4}$
We have two possible values for $x$:
Case 1: Using the '+' sign
$x = \frac{-1 + 65}{4} = \frac{64}{4} = 16$
Case 2: Using the '-' sign
$x = \frac{-1 - 65}{4} = \frac{-66}{4} = -\frac{33}{2} = -16.5$
Since $x$ represents the breadth of the plot, it must be a positive quantity. Therefore, we reject $x = -16.5$.
The breadth of the plot is $x = 16$ metres.
Now, calculate the length:
Length = $2x + 1 = 2(16) + 1 = 32 + 1 = 33$ metres.
Final Answer:
The dimensions of the rectangular plot are:
Breadth = 16 metres
Length = 33 metres
Example 11. Find two consecutive odd positive integers, sum of whose squares is 290.
Answer:
Given:
Two consecutive odd positive integers.
The sum of the squares of these integers is 290.
To Find:
The two consecutive odd positive integers.
Solution:
Let the first odd positive integer be $x$.
Since the integers are consecutive odd integers, the difference between them is 2. Therefore, the next consecutive odd positive integer is $x + 2$.
According to the problem statement, the sum of the squares of these two integers is 290.
Square of the first integer = $x^2$.
Square of the second integer = $(x + 2)^2$.
The equation representing the condition is:
$x^2 + (x + 2)^2 = 290$
Expand the term $(x + 2)^2$ using the identity $(a+b)^2 = a^2 + 2ab + b^2$:
$(x + 2)^2 = x^2 + 2(x)(2) + 2^2 = x^2 + 4x + 4$
Substitute this back into the equation:
$x^2 + (x^2 + 4x + 4) = 290$
Combine like terms:
$2x^2 + 4x + 4 = 290$
Subtract 290 from both sides to set the equation to zero:
$2x^2 + 4x + 4 - 290 = 0$
$2x^2 + 4x - 286 = 0$
Divide the entire equation by 2 to simplify:
$\frac{2x^2}{2} + \frac{4x}{2} - \frac{286}{2} = \frac{0}{2}$
$x^2 + 2x - 143 = 0$
Now, we solve this quadratic equation. We can use either factorisation or the quadratic formula.
Method 1: Factorisation
We need to find two numbers whose product is $1 \times (-143) = -143$ and whose sum is $2$.
Let's find factors of 143. $143 = 11 \times 13$.
The pair of factors whose difference is 2 is 11 and 13.
Since the sum is positive (+2), the numbers must be 13 and -11.
Split the middle term ($2x$):
$x^2 + 13x - 11x - 143 = 0$
Factor by grouping:
$(x^2 + 13x) + (-11x - 143) = 0$
$x(x + 13) - 11(x + 13) = 0$
Factor out the common binomial factor $(x + 13)$:
$(x + 13)(x - 11) = 0$
Using the Zero Product Property:
Either $x + 13 = 0 \implies x = -13$
Or $x - 11 = 0 \implies x = 11$
Method 2: Quadratic Formula
For the equation $x^2 + 2x - 143 = 0$, we have $a=1, b=2, c=-143$.
The quadratic formula is $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (2)^2 - 4(1)(-143) = 4 + 572 = 576$.
$x = \frac{-2 \pm \sqrt{576}}{2(1)}$
$x = \frac{-2 \pm 24}{2}$
Case 1: $x = \frac{-2 + 24}{2} = \frac{22}{2} = 11$
Case 2: $x = \frac{-2 - 24}{2} = \frac{-26}{2} = -13$
Interpreting the result:
The problem asks for positive odd integers. Therefore, $x = -13$ is rejected.
The first positive odd integer is $x = 11$.
The second consecutive odd positive integer is $x + 2 = 11 + 2 = 13$.
Check:
The integers are 11 and 13. They are consecutive, odd, and positive.
Sum of their squares = $11^2 + 13^2 = 121 + 169 = 290$. (Correct)
Final Answer:
The two consecutive odd positive integers are $\mathbf{11}$ and $\mathbf{13}$.
Example 12. A rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 square metres more than the area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude 12 m (see Fig. 4.3). Find its length and breadth.
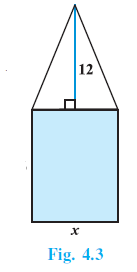
Answer:
Given:
A rectangular park.
Breadth of the rectangular park ($b$) = Length ($l$) - 3 m.
An isosceles triangular park.
Base of the triangular park = Breadth ($b$) of the rectangular park.
Altitude of the triangular park = 12 m.
Area of the rectangular park ($A_r$) = Area of the triangular park ($A_t$) + 4 m2.
To Find:
The length ($l$) and breadth ($b$) of the rectangular park.
Solution:
Let the length of the rectangular park be $l$ metres.
Given that the breadth is 3 m less than its length, the breadth $b = (l - 3)$ metres.
Area of the rectangular park, $A_r = \text{Length} \times \text{Breadth} = l \times (l - 3)$.
$A_r = l^2 - 3l$.
Now, consider the isosceles triangular park.
Base of the triangle = Breadth of the rectangle = $b = (l - 3)$ metres.
Altitude of the triangle = 12 m.
Area of the triangular park, $A_t = \frac{1}{2} \times \text{Base} \times \text{Altitude}$.
$A_t = \frac{1}{2} \times (l - 3) \times 12$
$A_t = 6(l - 3)$
$A_t = 6l - 18$.
According to the problem, the area of the rectangular park is 4 square metres more than the area of the triangular park:
$A_r = A_t + 4$
Substitute the expressions for $A_r$ and $A_t$:
$l^2 - 3l = (6l - 18) + 4$
$l^2 - 3l = 6l - 14$
Rearrange the terms to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$l^2 - 3l - 6l + 14 = 0$
$l^2 - 9l + 14 = 0$
Now, solve this quadratic equation for $l$. We can use the factorisation method.
We need two numbers whose product is $1 \times 14 = 14$ and whose sum is $-9$.
The pairs of factors of 14 are (1, 14), (2, 7), (-1, -14), (-2, -7).
The pair whose sum is -9 is -2 and -7.
Split the middle term ($-9l$):
$l^2 - 2l - 7l + 14 = 0$
Factor by grouping:
$(l^2 - 2l) + (-7l + 14) = 0$
$l(l - 2) - 7(l - 2) = 0$
Factor out the common binomial factor $(l - 2)$:
$(l - 2)(l - 7) = 0$
Using the Zero Product Property, set each factor equal to zero:
Either $l - 2 = 0 \implies l = 2$
Or $l - 7 = 0 \implies l = 7$
We need to check if both values of $l$ are valid by calculating the breadth $b = l - 3$.
Case 1: If $l = 2$ m
Breadth $b = l - 3 = 2 - 3 = -1$ m. Since the breadth cannot be negative, $l=2$ is not a valid solution.
Case 2: If $l = 7$ m
Breadth $b = l - 3 = 7 - 3 = 4$ m. This is a valid positive dimension.
So, the length of the rectangular park is 7 m and the breadth is 4 m.
Check:
Length = 7 m, Breadth = 4 m. (Breadth = 7 - 3 = 4 m).
Area of rectangle $A_r = 7 \times 4 = 28$ m2.
Base of triangle = 4 m, Altitude = 12 m.
Area of triangle $A_t = \frac{1}{2} \times 4 \times 12 = 24$ m2.
Is $A_r = A_t + 4$? Yes, $28 = 24 + 4$. The conditions are satisfied.
Final Answer:
The dimensions of the rectangular park are:
Length = 7 metres
Breadth = 4 metres
Example 13. Find the roots of the following quadratic equations, if they exist, using the quadratic formula:
(i) 3x2 - 5x + 2 = 0
(ii) x2 + 4x + 5 = 0
(iii) 2x2 - 2$\sqrt{2}$ x + 1 = 0
Answer:
General Concept: Quadratic Formula
For a quadratic equation in the standard form $ax^2 + bx + c = 0$ (where $a \neq 0$), the roots are given by the quadratic formula:
$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
The expression $D = b^2 - 4ac$ is called the discriminant.
- If $D > 0$, the equation has two distinct real roots.
- If $D = 0$, the equation has two equal real roots (or one real root).
- If $D < 0$, the equation has no real roots.
Solution (i): $3x^2 - 5x + 2 = 0$
Given equation: $3x^2 - 5x + 2 = 0$.
Comparing with $ax^2 + bx + c = 0$, we have:
$a = 3$, $b = -5$, $c = 2$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (-5)^2 - 4(3)(2)$
$D = 25 - 24$
$D = 1$
Since $D = 1 > 0$, the equation has two distinct real roots.
Now, apply the quadratic formula:
$x = \frac{-(-5) \pm \sqrt{1}}{2(3)}$
$x = \frac{5 \pm 1}{6}$
The two roots are:
$x_1 = \frac{5 + 1}{6} = \frac{6}{6} = 1$
$x_2 = \frac{5 - 1}{6} = \frac{4}{6} = \frac{2}{3}$
Conclusion: The roots of the equation $3x^2 - 5x + 2 = 0$ are $\mathbf{1}$ and $\mathbf{\frac{2}{3}}$.
Solution (ii): $x^2 + 4x + 5 = 0$
Given equation: $x^2 + 4x + 5 = 0$.
Comparing with $ax^2 + bx + c = 0$, we have:
$a = 1$, $b = 4$, $c = 5$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (4)^2 - 4(1)(5)$
$D = 16 - 20$
$D = -4$
Since $D = -4 < 0$, the discriminant is negative.
Conclusion: The equation $x^2 + 4x + 5 = 0$ has no real roots.
Solution (iii): $2x^2 - 2\sqrt{2}x + 1 = 0$
Given equation: $2x^2 - 2\sqrt{2}x + 1 = 0$.
Comparing with $ax^2 + bx + c = 0$, we have:
$a = 2$, $b = -2\sqrt{2}$, $c = 1$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (-2\sqrt{2})^2 - 4(2)(1)$
$D = (4 \times 2) - 8$
$D = 8 - 8$
$D = 0$
Since $D = 0$, the equation has two equal real roots (or one real root).
Now, apply the quadratic formula:
$x = \frac{-(-2\sqrt{2}) \pm \sqrt{0}}{2(2)}$
$x = \frac{2\sqrt{2} \pm 0}{4}$
$x = \frac{2\sqrt{2}}{4}$
$x = \frac{\sqrt{2}}{2}$
The roots are equal.
Conclusion: The roots of the equation $2x^2 - 2\sqrt{2}x + 1 = 0$ are $\mathbf{\frac{\sqrt{2}}{2}}$ and $\mathbf{\frac{\sqrt{2}}{2}}$ (or simply $\frac{\sqrt{2}}{2}$ as a repeated root).
Example 14. Find the roots of the following equations:
(i) x + $\frac{1}{x}$ = 3 , x ≠ 0
(ii) $\frac{1}{x}$ - $\frac{1}{x - 2}$ = 3, x ≠ 0,2
Answer:
Solution (i): $x + \frac{1}{x} = 3$, $x \neq 0$
Given equation: $x + \frac{1}{x} = 3$. The condition $x \neq 0$ is given because division by zero is undefined.
To Find: Roots of the equation.
Solution:
Multiply the entire equation by $x$ to eliminate the fraction:
$x \times (x + \frac{1}{x}) = x \times 3$
$x^2 + x \times \frac{1}{x} = 3x$
$x^2 + 1 = 3x$
Rearrange the terms to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$x^2 - 3x + 1 = 0$
Now, we use the quadratic formula to find the roots.
Comparing with $ax^2 + bx + c = 0$, we have:
$a = 1$, $b = -3$, $c = 1$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (-3)^2 - 4(1)(1)$
$D = 9 - 4$
$D = 5$
Since $D = 5 > 0$, the equation has two distinct real roots.
Apply the quadratic formula: $x = \frac{-b \pm \sqrt{D}}{2a}$
$x = \frac{-(-3) \pm \sqrt{5}}{2(1)}$
$x = \frac{3 \pm \sqrt{5}}{2}$
The two roots are $x_1 = \frac{3 + \sqrt{5}}{2}$ and $x_2 = \frac{3 - \sqrt{5}}{2}$.
Neither of these roots is 0, so they are valid solutions.
Conclusion: The roots of the equation $x + \frac{1}{x} = 3$ are $\mathbf{\frac{3 + \sqrt{5}}{2}}$ and $\mathbf{\frac{3 - \sqrt{5}}{2}}$.
Solution (ii): $\frac{1}{x} - \frac{1}{x - 2} = 3$, $x \neq 0, 2$
Given equation: $\frac{1}{x} - \frac{1}{x - 2} = 3$. The conditions $x \neq 0$ and $x \neq 2$ are given because they would lead to division by zero.
To Find: Roots of the equation.
Solution:
Find a common denominator for the left-hand side (LHS), which is $x(x - 2)$:
$\frac{1(x - 2)}{x(x - 2)} - \frac{1(x)}{x(x - 2)} = 3$
$\frac{(x - 2) - x}{x(x - 2)} = 3$
Simplify the numerator:
$\frac{-2}{x(x - 2)} = 3$
Expand the denominator:
$\frac{-2}{x^2 - 2x} = 3$
Multiply both sides by $(x^2 - 2x)$ to eliminate the fraction (assuming $x \neq 0, 2$):
$-2 = 3(x^2 - 2x)$
$-2 = 3x^2 - 6x$
Rearrange the terms to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$3x^2 - 6x + 2 = 0$
Now, we use the quadratic formula to find the roots.
Comparing with $ax^2 + bx + c = 0$, we have:
$a = 3$, $b = -6$, $c = 2$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (-6)^2 - 4(3)(2)$
$D = 36 - 24$
$D = 12$
Since $D = 12 > 0$, the equation has two distinct real roots.
Apply the quadratic formula: $x = \frac{-b \pm \sqrt{D}}{2a}$
$x = \frac{-(-6) \pm \sqrt{12}}{2(3)}$
$x = \frac{6 \pm \sqrt{4 \times 3}}{6}$
$x = \frac{6 \pm 2\sqrt{3}}{6}$
Factor out 2 from the numerator:
$x = \frac{2(3 \pm \sqrt{3})}{6}$
Simplify by cancelling the common factor 2:
$x = \frac{3 \pm \sqrt{3}}{3}$
The two roots are $x_1 = \frac{3 + \sqrt{3}}{3}$ and $x_2 = \frac{3 - \sqrt{3}}{3}$.
Neither of these roots is 0 or 2, so they are valid solutions.
Conclusion: The roots of the equation $\frac{1}{x} - \frac{1}{x - 2} = 3$ are $\mathbf{\frac{3 + \sqrt{3}}{3}}$ and $\mathbf{\frac{3 - \sqrt{3}}{3}}$.
Example 15. A motor boat whose speed is 18 km/h in still water takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Answer:
Given:
- Speed of the motor boat in still water = 18 km/h.
- Distance to travel upstream and downstream = 24 km.
- Time taken for the upstream journey is 1 hour more than the time taken for the downstream journey.
To Find:
The speed of the stream.
Solution:
Let the speed of the stream be $x$ km/h.
The speed of the boat in still water is 18 km/h.
Speed Downstream: When the boat travels downstream (in the direction of the stream), the speed of the stream adds to the speed of the boat.
Speed downstream = (Speed of boat in still water) + (Speed of stream) = $(18 + x)$ km/h.
Speed Upstream: When the boat travels upstream (against the direction of the stream), the speed of the stream subtracts from the speed of the boat.
Speed upstream = (Speed of boat in still water) - (Speed of stream) = $(18 - x)$ km/h.
We must have $18 - x > 0$ for the boat to travel upstream, so $x < 18$. Also, speed $x$ must be positive.
The distance for both journeys is 24 km.
We know that Time = $\frac{\text{Distance}}{\text{Speed}}$.
Time taken for the downstream journey ($T_{down}$) = $\frac{24}{18 + x}$ hours.
Time taken for the upstream journey ($T_{up}$) = $\frac{24}{18 - x}$ hours.
According to the problem statement, the time taken for the upstream journey is 1 hour more than the time taken for the downstream journey:
$T_{up} = T_{down} + 1$
$\frac{24}{18 - x} = \frac{24}{18 + x} + 1$
Rearrange the equation to solve for $x$:
$\frac{24}{18 - x} - \frac{24}{18 + x} = 1$
Factor out 24 from the left-hand side:
$24 \left( \frac{1}{18 - x} - \frac{1}{18 + x} \right) = 1$
Find a common denominator inside the parentheses, which is $(18 - x)(18 + x) = 18^2 - x^2 = 324 - x^2$.
$24 \left( \frac{(18 + x) - (18 - x)}{(18 - x)(18 + x)} \right) = 1$
$24 \left( \frac{18 + x - 18 + x}{324 - x^2} \right) = 1$
$24 \left( \frac{2x}{324 - x^2} \right) = 1$
$\frac{48x}{324 - x^2} = 1$
Multiply both sides by $(324 - x^2)$:
$48x = 324 - x^2$
Rearrange the terms to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$x^2 + 48x - 324 = 0$
Now, solve this quadratic equation using the quadratic formula: $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$.
Here, $a = 1$, $b = 48$, $c = -324$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (48)^2 - 4(1)(-324)$
$D = 2304 + 1296$
$D = 3600$
Since $D > 0$, there are two distinct real roots.
$x = \frac{-48 \pm \sqrt{3600}}{2(1)}$
$x = \frac{-48 \pm 60}{2}$
The two possible values for $x$ are:
$x_1 = \frac{-48 + 60}{2} = \frac{12}{2} = 6$
$x_2 = \frac{-48 - 60}{2} = \frac{-108}{2} = -54$
Since the speed of the stream ($x$) cannot be negative, we discard the solution $x = -54$.
Therefore, the speed of the stream is $x = 6$ km/h.
This value satisfies the condition $0 < x < 18$.
Final Answer:
The speed of the stream is $\mathbf{6}$ km/h.
Exercise 4.3
Question 1. Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
(i) 2x2 – 7x + 3 = 0
(ii) 2x2 + x – 4 = 0
(iii) 4x2 + 4$\sqrt{3}$ x + 3 = 0
(iv) 2x2 + x + 4 = 0
Answer:
Solution (i): $2x^2 - 7x + 3 = 0$
Given equation: $2x^2 - 7x + 3 = 0$.
To Find: Roots by completing the square.
Solution:
First, check if real roots exist using the discriminant $D = b^2 - 4ac$.
Here $a=2$, $b=-7$, $c=3$.
$D = (-7)^2 - 4(2)(3) = 49 - 24 = 25$.
Since $D = 25 > 0$, real and distinct roots exist.
Step 1: Divide by the coefficient of $x^2$ (which is 2).
$x^2 - \frac{7}{2}x + \frac{3}{2} = 0$
Step 2: Move the constant term to the RHS.
$x^2 - \frac{7}{2}x = -\frac{3}{2}$
Step 3: Take half of the coefficient of $x$, square it, and add to both sides.
Coefficient of $x$ is $-\frac{7}{2}$. Half is $\frac{1}{2} \times (-\frac{7}{2}) = -\frac{7}{4}$.
Square of half the coefficient is $(-\frac{7}{4})^2 = \frac{49}{16}$.
Add $\frac{49}{16}$ to both sides:
$x^2 - \frac{7}{2}x + \frac{49}{16} = -\frac{3}{2} + \frac{49}{16}$
Step 4: Factor the LHS as a perfect square.
$(x - \frac{7}{4})^2 = -\frac{3 \times 8}{2 \times 8} + \frac{49}{16}$
$(x - \frac{7}{4})^2 = -\frac{24}{16} + \frac{49}{16}$
$(x - \frac{7}{4})^2 = \frac{-24 + 49}{16}$
$(x - \frac{7}{4})^2 = \frac{25}{16}$
Step 5: Take the square root of both sides.
$x - \frac{7}{4} = \pm \sqrt{\frac{25}{16}}$
$x - \frac{7}{4} = \pm \frac{5}{4}$
Step 6: Solve for $x$.
$x = \frac{7}{4} \pm \frac{5}{4}$
Two possible roots:
$x_1 = \frac{7}{4} + \frac{5}{4} = \frac{7+5}{4} = \frac{12}{4} = 3$
$x_2 = \frac{7}{4} - \frac{5}{4} = \frac{7-5}{4} = \frac{2}{4} = \frac{1}{2}$
Conclusion: The roots of the equation $2x^2 - 7x + 3 = 0$ are $\mathbf{3}$ and $\mathbf{\frac{1}{2}}$.
Solution (ii): $2x^2 + x - 4 = 0$
Given equation: $2x^2 + x - 4 = 0$.
To Find: Roots by completing the square.
Solution:
First, check if real roots exist using the discriminant $D = b^2 - 4ac$.
Here $a=2$, $b=1$, $c=-4$.
$D = (1)^2 - 4(2)(-4) = 1 - (-32) = 1 + 32 = 33$.
Since $D = 33 > 0$, real and distinct roots exist.
Step 1: Divide by the coefficient of $x^2$ (which is 2).
$x^2 + \frac{1}{2}x - \frac{4}{2} = 0$
$x^2 + \frac{1}{2}x - 2 = 0$
Step 2: Move the constant term to the RHS.
$x^2 + \frac{1}{2}x = 2$
Step 3: Take half of the coefficient of $x$, square it, and add to both sides.
Coefficient of $x$ is $\frac{1}{2}$. Half is $\frac{1}{2} \times \frac{1}{2} = \frac{1}{4}$.
Square of half the coefficient is $(\frac{1}{4})^2 = \frac{1}{16}$.
Add $\frac{1}{16}$ to both sides:
$x^2 + \frac{1}{2}x + \frac{1}{16} = 2 + \frac{1}{16}$
Step 4: Factor the LHS as a perfect square.
$(x + \frac{1}{4})^2 = \frac{2 \times 16}{1 \times 16} + \frac{1}{16}$
$(x + \frac{1}{4})^2 = \frac{32}{16} + \frac{1}{16}$
$(x + \frac{1}{4})^2 = \frac{33}{16}$
Step 5: Take the square root of both sides.
$x + \frac{1}{4} = \pm \sqrt{\frac{33}{16}}$
$x + \frac{1}{4} = \pm \frac{\sqrt{33}}{4}$
Step 6: Solve for $x$.
$x = -\frac{1}{4} \pm \frac{\sqrt{33}}{4}$
$x = \frac{-1 \pm \sqrt{33}}{4}$
Two possible roots:
$x_1 = \frac{-1 + \sqrt{33}}{4}$
$x_2 = \frac{-1 - \sqrt{33}}{4}$
Conclusion: The roots of the equation $2x^2 + x - 4 = 0$ are $\mathbf{\frac{-1 + \sqrt{33}}{4}}$ and $\mathbf{\frac{-1 - \sqrt{33}}{4}}$.
Solution (iii): $4x^2 + 4\sqrt{3}x + 3 = 0$
Given equation: $4x^2 + 4\sqrt{3}x + 3 = 0$.
To Find: Roots by completing the square.
Solution:
First, check if real roots exist using the discriminant $D = b^2 - 4ac$.
Here $a=4$, $b=4\sqrt{3}$, $c=3$.
$D = (4\sqrt{3})^2 - 4(4)(3) = (16 \times 3) - 48 = 48 - 48 = 0$.
Since $D = 0$, real and equal roots exist.
Step 1: Divide by the coefficient of $x^2$ (which is 4).
$x^2 + \frac{4\sqrt{3}}{4}x + \frac{3}{4} = 0$
$x^2 + \sqrt{3}x + \frac{3}{4} = 0$
Step 2: Move the constant term to the RHS.
$x^2 + \sqrt{3}x = -\frac{3}{4}$
Step 3: Take half of the coefficient of $x$, square it, and add to both sides.
Coefficient of $x$ is $\sqrt{3}$. Half is $\frac{\sqrt{3}}{2}$.
Square of half the coefficient is $(\frac{\sqrt{3}}{2})^2 = \frac{3}{4}$.
Add $\frac{3}{4}$ to both sides:
$x^2 + \sqrt{3}x + \frac{3}{4} = -\frac{3}{4} + \frac{3}{4}$
Step 4: Factor the LHS as a perfect square.
$(x + \frac{\sqrt{3}}{2})^2 = 0$
Step 5: Take the square root of both sides.
$x + \frac{\sqrt{3}}{2} = \pm \sqrt{0}$
$x + \frac{\sqrt{3}}{2} = 0$
Step 6: Solve for $x$.
$x = -\frac{\sqrt{3}}{2}$
Since the discriminant was 0, we get two equal roots.
Conclusion: The roots of the equation $4x^2 + 4\sqrt{3}x + 3 = 0$ are $\mathbf{-\frac{\sqrt{3}}{2}}$ and $\mathbf{-\frac{\sqrt{3}}{2}}$.
Solution (iv): $2x^2 + x + 4 = 0$
Given equation: $2x^2 + x + 4 = 0$.
To Find: Roots by completing the square.
Solution:
First, check if real roots exist using the discriminant $D = b^2 - 4ac$.
Here $a=2$, $b=1$, $c=4$.
$D = (1)^2 - 4(2)(4) = 1 - 32 = -31$.
Since $D = -31 < 0$, the discriminant is negative.
Therefore, the equation has no real roots.
Attempting to complete the square (for illustration):
Divide by 2: $x^2 + \frac{1}{2}x + 2 = 0$
Move constant term: $x^2 + \frac{1}{2}x = -2$
Half of coefficient of $x$ is $\frac{1}{4}$. Square is $\frac{1}{16}$. Add to both sides:
$x^2 + \frac{1}{2}x + \frac{1}{16} = -2 + \frac{1}{16}$
Factor LHS: $(x + \frac{1}{4})^2 = -\frac{32}{16} + \frac{1}{16}$
$(x + \frac{1}{4})^2 = -\frac{31}{16}$
As shown here, the square of a real expression $(x + \frac{1}{4})^2$ is equal to a negative number $(-\frac{31}{16})$. This is impossible for real numbers.
Conclusion: The equation $2x^2 + x + 4 = 0$ has no real roots.
Question 2. Find the roots of the quadratic equations given in Q.1 above by applying the quadratic formula.
Answer:
General Concept: Quadratic Formula
For a quadratic equation in the standard form $ax^2 + bx + c = 0$ (where $a \neq 0$), the roots are given by the quadratic formula:
$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
The expression $D = b^2 - 4ac$ is the discriminant, which determines the nature of the roots:
- If $D > 0$, there are two distinct real roots.
- If $D = 0$, there are two equal real roots (one real root).
- If $D < 0$, there are no real roots.
Solution (i): $2x^2 - 7x + 3 = 0$
Given equation: $2x^2 - 7x + 3 = 0$.
Comparing with $ax^2 + bx + c = 0$, we have:
$a = 2$, $b = -7$, $c = 3$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (-7)^2 - 4(2)(3)$
$D = 49 - 24$
$D = 25$
Since $D = 25 > 0$, the equation has two distinct real roots.
Apply the quadratic formula:
$x = \frac{-(-7) \pm \sqrt{25}}{2(2)}$
$x = \frac{7 \pm 5}{4}$
The two roots are:
$x_1 = \frac{7 + 5}{4} = \frac{12}{4} = 3$
$x_2 = \frac{7 - 5}{4} = \frac{2}{4} = \frac{1}{2}$
Conclusion: The roots are $\mathbf{3}$ and $\mathbf{\frac{1}{2}}$.
Solution (ii): $2x^2 + x - 4 = 0$
Given equation: $2x^2 + x - 4 = 0$.
Comparing with $ax^2 + bx + c = 0$, we have:
$a = 2$, $b = 1$, $c = -4$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (1)^2 - 4(2)(-4)$
$D = 1 - (-32)$
$D = 1 + 32 = 33$
Since $D = 33 > 0$, the equation has two distinct real roots.
Apply the quadratic formula:
$x = \frac{-(1) \pm \sqrt{33}}{2(2)}$
$x = \frac{-1 \pm \sqrt{33}}{4}$
The two roots are:
$x_1 = \frac{-1 + \sqrt{33}}{4}$
$x_2 = \frac{-1 - \sqrt{33}}{4}$
Conclusion: The roots are $\mathbf{\frac{-1 + \sqrt{33}}{4}}$ and $\mathbf{\frac{-1 - \sqrt{33}}{4}}$.
Solution (iii): $4x^2 + 4\sqrt{3}x + 3 = 0$
Given equation: $4x^2 + 4\sqrt{3}x + 3 = 0$.
Comparing with $ax^2 + bx + c = 0$, we have:
$a = 4$, $b = 4\sqrt{3}$, $c = 3$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (4\sqrt{3})^2 - 4(4)(3)$
$D = (16 \times 3) - 48$
$D = 48 - 48 = 0$
Since $D = 0$, the equation has two equal real roots.
Apply the quadratic formula:
$x = \frac{-(4\sqrt{3}) \pm \sqrt{0}}{2(4)}$
$x = \frac{-4\sqrt{3} \pm 0}{8}$
$x = \frac{-4\sqrt{3}}{8}$
$x = -\frac{\sqrt{3}}{2}$
The two equal roots are $x_1 = x_2 = -\frac{\sqrt{3}}{2}$.
Conclusion: The roots are $\mathbf{-\frac{\sqrt{3}}{2}}$ and $\mathbf{-\frac{\sqrt{3}}{2}}$.
Solution (iv): $2x^2 + x + 4 = 0$
Given equation: $2x^2 + x + 4 = 0$.
Comparing with $ax^2 + bx + c = 0$, we have:
$a = 2$, $b = 1$, $c = 4$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (1)^2 - 4(2)(4)$
$D = 1 - 32$
$D = -31$
Since $D = -31 < 0$, the discriminant is negative.
Conclusion: The equation $2x^2 + x + 4 = 0$ has no real roots.
Question 3. Find the roots of the following equations:
(i) x - $\frac{1}{x}$ = 3 , x ≠ 0
(ii) $\frac{1}{x + 4}$ - $\frac{1}{x - 7}$ = $\frac{11}{30}$ , x ≠ -4 , 7
Answer:
Solution (i): $x - \frac{1}{x} = 3$, $x \neq 0$
Given equation: $x - \frac{1}{x} = 3$. The condition $x \neq 0$ ensures the expression is defined.
To Find: Roots of the equation.
Solution:
Multiply the entire equation by $x$ to eliminate the fraction:
$x \times (x - \frac{1}{x}) = x \times 3$
$x^2 - x \times \frac{1}{x} = 3x$
$x^2 - 1 = 3x$
Rearrange the terms into the standard quadratic form $ax^2 + bx + c = 0$:
$x^2 - 3x - 1 = 0$
We will use the quadratic formula to find the roots. Comparing with $ax^2 + bx + c = 0$, we have:
$a = 1$, $b = -3$, $c = -1$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (-3)^2 - 4(1)(-1)$
$D = 9 - (-4)$
$D = 9 + 4 = 13$
Since $D = 13 > 0$, the equation has two distinct real roots.
Apply the quadratic formula: $x = \frac{-b \pm \sqrt{D}}{2a}$
$x = \frac{-(-3) \pm \sqrt{13}}{2(1)}$
$x = \frac{3 \pm \sqrt{13}}{2}$
The two roots are $x_1 = \frac{3 + \sqrt{13}}{2}$ and $x_2 = \frac{3 - \sqrt{13}}{2}$.
These roots are not equal to 0, so they are valid.
Conclusion: The roots of the equation $x - \frac{1}{x} = 3$ are $\mathbf{\frac{3 + \sqrt{13}}{2}}$ and $\mathbf{\frac{3 - \sqrt{13}}{2}}$.
Solution (ii): $\frac{1}{x + 4} - \frac{1}{x - 7} = \frac{11}{30}$, $x \neq -4, 7$
Given equation: $\frac{1}{x + 4} - \frac{1}{x - 7} = \frac{11}{30}$. The conditions $x \neq -4$ and $x \neq 7$ ensure the denominators are non-zero.
To Find: Roots of the equation.
Solution:
Find a common denominator for the left-hand side (LHS), which is $(x + 4)(x - 7)$:
$\frac{1(x - 7)}{(x + 4)(x - 7)} - \frac{1(x + 4)}{(x + 4)(x - 7)} = \frac{11}{30}$
$\frac{(x - 7) - (x + 4)}{(x + 4)(x - 7)} = \frac{11}{30}$
Simplify the numerator and expand the denominator:
$\frac{x - 7 - x - 4}{x(x - 7) + 4(x - 7)} = \frac{11}{30}$
$\frac{-11}{x^2 - 7x + 4x - 28} = \frac{11}{30}$
$\frac{-11}{x^2 - 3x - 28} = \frac{11}{30}$
Divide both sides by 11 (since $11 \neq 0$):
$\frac{-1}{x^2 - 3x - 28} = \frac{1}{30}$
Cross-multiply:
$-1 \times 30 = 1 \times (x^2 - 3x - 28)$
$-30 = x^2 - 3x - 28$
Rearrange the terms into the standard quadratic form $ax^2 + bx + c = 0$:
$x^2 - 3x - 28 + 30 = 0$
$x^2 - 3x + 2 = 0$
We can solve this quadratic equation by factorisation.
We need two numbers whose product is $1 \times 2 = 2$ and whose sum is $-3$. The numbers are -1 and -2.
Split the middle term:
$x^2 - 1x - 2x + 2 = 0$
Factor by grouping:
$x(x - 1) - 2(x - 1) = 0$
Factor out the common binomial factor $(x - 1)$:
$(x - 1)(x - 2) = 0$
Using the Zero Product Property, set each factor equal to zero:
Either $x - 1 = 0 \implies x = 1$
Or $x - 2 = 0 \implies x = 2$
The roots are 1 and 2. Both are valid as they are not equal to -4 or 7.
Conclusion: The roots of the equation $\frac{1}{x + 4} - \frac{1}{x - 7} = \frac{11}{30}$ are $\mathbf{1}$ and $\mathbf{2}$.
Question 4. The sum of the reciprocals of Rehman’s ages, (in years) 3 years ago and 5 years from now is $\frac{1}{3}$ . Find his present age.
Answer:
Given:
The sum of the reciprocals of Rehman's age 3 years ago and his age 5 years from now is $\frac{1}{3}$.
To Find:
Rehman's present age.
Solution:
Let Rehman's present age be $x$ years.
Rehman's age 3 years ago = $(x - 3)$ years.
Rehman's age 5 years from now = $(x + 5)$ years.
The reciprocals of these ages are:
Reciprocal of age 3 years ago = $\frac{1}{x - 3}$. (We must have $x > 3$ for age to be positive).
Reciprocal of age 5 years from now = $\frac{1}{x + 5}$.
According to the problem statement, the sum of these reciprocals is $\frac{1}{3}$:
$\frac{1}{x - 3} + \frac{1}{x + 5} = \frac{1}{3}$
To solve this equation, find a common denominator for the left-hand side (LHS), which is $(x - 3)(x + 5)$:
$\frac{1(x + 5)}{(x - 3)(x + 5)} + \frac{1(x - 3)}{(x - 3)(x + 5)} = \frac{1}{3}$
$\frac{(x + 5) + (x - 3)}{(x - 3)(x + 5)} = \frac{1}{3}$
Simplify the numerator and expand the denominator:
$\frac{2x + 2}{x^2 + 5x - 3x - 15} = \frac{1}{3}$
$\frac{2x + 2}{x^2 + 2x - 15} = \frac{1}{3}$
Cross-multiply:
$3(2x + 2) = 1(x^2 + 2x - 15)$
$6x + 6 = x^2 + 2x - 15$
Rearrange the terms to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$0 = x^2 + 2x - 15 - 6x - 6$
$x^2 - 4x - 21 = 0$
Now, solve this quadratic equation by factorisation.
We need two numbers whose product is $1 \times (-21) = -21$ and whose sum is $-4$. The numbers are $-7$ and $3$.
Split the middle term:
$x^2 - 7x + 3x - 21 = 0$
Factor by grouping:
$x(x - 7) + 3(x - 7) = 0$
Factor out the common binomial factor $(x - 7)$:
$(x - 7)(x + 3) = 0$
Using the Zero Product Property, set each factor equal to zero:
Either $x - 7 = 0 \implies x = 7$
Or $x + 3 = 0 \implies x = -3$
Since age ($x$) cannot be negative, we reject the solution $x = -3$.
Therefore, Rehman's present age is $x = 7$ years.
Check: If present age is 7, age 3 years ago was 4, age 5 years from now is 12. Sum of reciprocals = $\frac{1}{4} + \frac{1}{12} = \frac{3+1}{12} = \frac{4}{12} = \frac{1}{3}$. This matches the given condition.
Final Answer:
Rehman's present age is $\mathbf{7}$ years.
Question 5. In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
Answer:
Given:
- Sum of Shefali's marks in Mathematics and English = 30.
- If Mathematics marks were 2 more and English marks were 3 less, the product of these marks would be 210.
To Find:
Shefali's marks in Mathematics and English.
Solution:
Let Shefali's marks in Mathematics be $M$.
Let Shefali's marks in English be $E$.
From the first condition, the sum of marks is 30:
$M + E = 30$
...(i)
From this, we can express the marks in English in terms of marks in Mathematics:
$E = 30 - M$
Now consider the second condition:
If she got 2 marks more in Mathematics, her marks would be $M + 2$.
If she got 3 marks less in English, her marks would be $E - 3$.
Substituting $E = 30 - M$ into the modified English marks:
Modified English marks = $(30 - M) - 3 = 27 - M$.
The product of these modified marks is 210:
$(M + 2)(27 - M) = 210$
Expand the equation:
$M(27 - M) + 2(27 - M) = 210$
$27M - M^2 + 54 - 2M = 210$
Combine like terms:
$-M^2 + (27M - 2M) + 54 = 210$
$-M^2 + 25M + 54 = 210$
Move all terms to one side to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$-M^2 + 25M + 54 - 210 = 0$
$-M^2 + 25M - 156 = 0$
Multiply the entire equation by -1 to make the leading coefficient positive:
$M^2 - 25M + 156 = 0$
Now, solve this quadratic equation for $M$ by factorisation.
We need two numbers whose product is $1 \times 156 = 156$ and whose sum is $-25$. Since the product is positive and the sum is negative, both numbers must be negative.
Let's find factors of 156: $156 = 2 \times 78 = 2 \times 2 \times 39 = 2 \times 2 \times 3 \times 13$.
Possible pairs of factors: (1, 156), (2, 78), (3, 52), (4, 39), (6, 26), (12, 13).
The pair whose sum is 25 is 12 and 13. So, the required numbers are -12 and -13.
Split the middle term:
$M^2 - 12M - 13M + 156 = 0$
Factor by grouping:
$M(M - 12) - 13(M - 12) = 0$
Factor out the common binomial factor $(M - 12)$:
$(M - 12)(M - 13) = 0$
Using the Zero Product Property, set each factor equal to zero:
Either $M - 12 = 0 \implies M = 12$
Or $M - 13 = 0 \implies M = 13$
Now, find the corresponding marks in English ($E = 30 - M$) for each case:
Case 1: If Mathematics marks $M = 12$
English marks $E = 30 - 12 = 18$.
Case 2: If Mathematics marks $M = 13$
English marks $E = 30 - 13 = 17$.
Both sets of marks are possible solutions.
Check Case 1: Maths=12, English=18. Modified: Maths=14, English=15. Product=$14 \times 15 = 210$. (Correct)
Check Case 2: Maths=13, English=17. Modified: Maths=15, English=14. Product=$15 \times 14 = 210$. (Correct)
Final Answer:
There are two possible sets of marks:
Either Shefali scored 12 marks in Mathematics and 18 marks in English.
Or Shefali scored 13 marks in Mathematics and 17 marks in English.
Question 6. The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
Answer:
Given:
- A rectangular field.
- Diagonal = Shorter side + 60 metres.
- Longer side = Shorter side + 30 metres.
To Find:
The lengths of the sides of the rectangular field (shorter side and longer side).
Solution:
Let the length of the shorter side of the rectangular field be $x$ metres.
According to the given conditions:
Longer side = $(x + 30)$ metres.
Diagonal = $(x + 60)$ metres.
In a rectangle, the two adjacent sides and the diagonal form a right-angled triangle, with the diagonal as the hypotenuse.
Applying the Pythagorean theorem:
$(\text{Shorter side})^2 + (\text{Longer side})^2 = (\text{Diagonal})^2$
Substitute the expressions in terms of $x$:
$x^2 + (x + 30)^2 = (x + 60)^2$
Expand the squared binomials using the identity $(a+b)^2 = a^2 + 2ab + b^2$:
$(x + 30)^2 = x^2 + 2(x)(30) + 30^2 = x^2 + 60x + 900$
$(x + 60)^2 = x^2 + 2(x)(60) + 60^2 = x^2 + 120x + 3600$
Substitute these expansions back into the Pythagorean equation:
$x^2 + (x^2 + 60x + 900) = x^2 + 120x + 3600$
Combine like terms on the left side:
$2x^2 + 60x + 900 = x^2 + 120x + 3600$
Move all terms to one side to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$(2x^2 - x^2) + (60x - 120x) + (900 - 3600) = 0$
$x^2 - 60x - 2700 = 0$
Now, solve this quadratic equation for $x$ by factorisation.
We need two numbers whose product is $-2700$ and whose sum is $-60$. The numbers are $-90$ and $30$.
Split the middle term:
$x^2 - 90x + 30x - 2700 = 0$
Factor by grouping:
$x(x - 90) + 30(x - 90) = 0$
Factor out the common binomial factor $(x - 90)$:
$(x - 90)(x + 30) = 0$
Using the Zero Product Property, set each factor equal to zero:
Either $x - 90 = 0 \implies x = 90$
Or $x + 30 = 0 \implies x = -30$
Since $x$ represents the length of a side, it cannot be negative. Therefore, we reject $x = -30$.
The shorter side of the field is $x = 90$ metres.
Calculate the length of the longer side:
Longer side = $x + 30 = 90 + 30 = 120$ metres.
Check:
Shorter side = 90 m, Longer side = 120 m.
Diagonal = $x + 60 = 90 + 60 = 150$ m.
Check Pythagorean theorem: $90^2 + 120^2 = 8100 + 14400 = 22500$.
Diagonal$^2 = 150^2 = 22500$. The condition holds.
Final Answer:
The sides of the rectangular field are $\mathbf{90}$ metres and $\mathbf{120}$ metres.
Question 7. The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.
Answer:
Given:
- Two numbers.
- The difference of their squares is 180.
- The square of the smaller number is 8 times the larger number.
To Find:
The two numbers.
Solution:
Let the larger number be $x$ and the smaller number be $y$.
According to the first condition, the difference of their squares is 180:
$x^2 - y^2 = 180$
...(i)
According to the second condition, the square of the smaller number ($y^2$) is 8 times the larger number ($x$):
$y^2 = 8x$
...(ii)
Now, substitute the expression for $y^2$ from equation (ii) into equation (i):
$x^2 - (8x) = 180$
Rearrange the terms to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$x^2 - 8x - 180 = 0$
Solve this quadratic equation for $x$. We can use the factorisation method.
We need two numbers whose product is $1 \times (-180) = -180$ and whose sum is $-8$.
Factors of 180 are: (1, 180), (2, 90), (3, 60), (4, 45), (5, 36), (6, 30), (9, 20), (10, 18), (12, 15).
We need a pair with a difference of 8, which is 10 and 18.
To get a sum of -8, the numbers must be $-18$ and $10$.
Split the middle term:
$x^2 - 18x + 10x - 180 = 0$
Factor by grouping:
$x(x - 18) + 10(x - 18) = 0$
Factor out the common binomial factor $(x - 18)$:
$(x - 18)(x + 10) = 0$
Using the Zero Product Property, set each factor equal to zero:
Either $x - 18 = 0 \implies x = 18$
Or $x + 10 = 0 \implies x = -10$
Now, find the corresponding values of $y$ using equation (ii), $y^2 = 8x$.
Case 1: If the larger number $x = 18$.
$y^2 = 8(18) = 144$
$y = \pm \sqrt{144}$
$y = \pm 12$.
In this case, the smaller number $y$ can be 12 or -12. Since $18 > 12$ and $18 > -12$, $x=18$ is indeed the larger number. The possible pairs of numbers are (18, 12) and (18, -12).
Case 2: If the larger number $x = -10$.
$y^2 = 8(-10) = -80$.
The square of a real number cannot be negative. Therefore, there is no real value for $y$ when $x = -10$. This case yields no real solutions.
So, the only possible pairs of real numbers are (18, 12) and (18, -12).
Check:
For (18, 12): $18^2 - 12^2 = 324 - 144 = 180$. $12^2 = 144 = 8 \times 18$. Both conditions hold.
For (18, -12): $18^2 - (-12)^2 = 324 - 144 = 180$. $(-12)^2 = 144 = 8 \times 18$. Both conditions hold.
Final Answer:
The two numbers are either $\mathbf{18}$ and $\mathbf{12}$, or $\mathbf{18}$ and $\mathbf{-12}$.
Question 8. A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Answer:
Given:
- Distance travelled by the train = 360 km.
- The train travels at a uniform speed.
- If the speed were 5 km/h more, the time taken would be 1 hour less.
To Find:
The uniform speed of the train.
Solution:
Let the uniform speed of the train be $x$ km/h.
The distance to be covered is 360 km.
We know that Time = $\frac{\text{Distance}}{\text{Speed}}$.
Time taken at the uniform speed ($T_1$) = $\frac{360}{x}$ hours.
If the speed had been 5 km/h more, the new speed would be $(x + 5)$ km/h.
Time taken at the new speed ($T_2$) = $\frac{360}{x + 5}$ hours.
According to the problem statement, the time taken at the new speed ($T_2$) is 1 hour less than the time taken at the original speed ($T_1$).
$T_2 = T_1 - 1$
Alternatively, $T_1 = T_2 + 1$.
Substituting the expressions for $T_1$ and $T_2$:
$\frac{360}{x} = \frac{360}{x + 5} + 1$
Rearrange the equation to solve for $x$:
$\frac{360}{x} - \frac{360}{x + 5} = 1$
Factor out 360 from the left-hand side:
$360 \left( \frac{1}{x} - \frac{1}{x + 5} \right) = 1$
Find a common denominator inside the parentheses, which is $x(x + 5)$.
$360 \left( \frac{(x + 5) - x}{x(x + 5)} \right) = 1$
$360 \left( \frac{x + 5 - x}{x^2 + 5x} \right) = 1$
$360 \left( \frac{5}{x^2 + 5x} \right) = 1$
$\frac{1800}{x^2 + 5x} = 1$
Multiply both sides by $(x^2 + 5x)$:
$1800 = x^2 + 5x$
Rearrange the terms to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$x^2 + 5x - 1800 = 0$
Now, solve this quadratic equation. We can use factorisation.
We need two numbers whose product is $-1800$ and whose sum is $5$. These numbers are $45$ and $-40$.
Split the middle term:
$x^2 + 45x - 40x - 1800 = 0$
Factor by grouping:
$x(x + 45) - 40(x + 45) = 0$
Factor out the common binomial factor $(x + 45)$:
$(x + 45)(x - 40) = 0$
Using the Zero Product Property, set each factor equal to zero:
Either $x + 45 = 0 \implies x = -45$
Or $x - 40 = 0 \implies x = 40$
Since the speed of the train ($x$) must be positive, we reject the solution $x = -45$.
Therefore, the uniform speed of the train is $x = 40$ km/h.
Check:
Original time = $360/40 = 9$ hours.
New speed = $40 + 5 = 45$ km/h.
New time = $360/45 = 8$ hours.
The new time is indeed 1 hour less than the original time ($8 = 9 - 1$).
Final Answer:
The speed of the train is $\mathbf{40}$ km/h.
Question 9. Two water taps together can fill a tank in $9\frac{3}{8}$ hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Answer:
Given:
- Combined time taken by two water taps to fill the tank = $9\frac{3}{8}$ hours.
- The tap with the larger diameter takes 10 hours less than the smaller one to fill the tank alone.
To Find:
The time taken by each tap to fill the tank separately.
Solution:
Let the time taken by the smaller tap to fill the tank alone be $x$ hours.
Since the larger tap takes 10 hours less than the smaller one, the time taken by the larger tap to fill the tank alone is $(x - 10)$ hours.
For the solution to be physically possible, both times must be positive, so $x > 0$ and $x - 10 > 0$, which implies $x > 10$.
Now, consider the rate at which each tap fills the tank (the fraction of the tank filled per hour).
Rate of the smaller tap = $\frac{1}{x}$ tank per hour.
Rate of the larger tap = $\frac{1}{x - 10}$ tank per hour.
When both taps work together, their rates add up.
Combined rate = Rate of smaller tap + Rate of larger tap = $\frac{1}{x} + \frac{1}{x - 10}$ tank per hour.
The combined time taken is given as $9\frac{3}{8}$ hours. Let's convert this to an improper fraction:
$9\frac{3}{8} = \frac{9 \times 8 + 3}{8} = \frac{72 + 3}{8} = \frac{75}{8}$ hours.
The combined rate is the reciprocal of the combined time:
Combined rate = $\frac{1}{\text{Combined Time}} = \frac{1}{75/8} = \frac{8}{75}$ tank per hour.
Now, equate the sum of individual rates to the combined rate:
$\frac{1}{x} + \frac{1}{x - 10} = \frac{8}{75}$
Find a common denominator for the left-hand side:
$\frac{(x - 10) + x}{x(x - 10)} = \frac{8}{75}$
$\frac{2x - 10}{x^2 - 10x} = \frac{8}{75}$
Cross-multiply:
$75(2x - 10) = 8(x^2 - 10x)$
$150x - 750 = 8x^2 - 80x$
Rearrange the terms into the standard quadratic form $ax^2 + bx + c = 0$:
$0 = 8x^2 - 80x - 150x + 750$
$8x^2 - 230x + 750 = 0$
Divide the entire equation by 2 to simplify:
$4x^2 - 115x + 375 = 0$
Solve this quadratic equation using the quadratic formula: $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$.
Here, $a = 4$, $b = -115$, $c = 375$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (-115)^2 - 4(4)(375)$
$D = 13225 - 16(375)$
$D = 13225 - 6000$
$D = 7225$
Apply the quadratic formula:
$x = \frac{-(-115) \pm \sqrt{7225}}{2(4)}$
$x = \frac{115 \pm 85}{8}$ (Since $\sqrt{7225} = 85$)
The two possible values for $x$ are:
$x_1 = \frac{115 + 85}{8} = \frac{200}{8} = 25$
$x_2 = \frac{115 - 85}{8} = \frac{30}{8} = \frac{15}{4} = 3.75$
We established earlier that $x$ must be greater than 10 ($x > 10$).
Therefore, $x = 3.75$ is not a valid solution.
The only valid solution is $x = 25$.
Time taken by the smaller tap = $x = 25$ hours.
Time taken by the larger tap = $x - 10 = 25 - 10 = 15$ hours.
Final Answer:
The time taken by the smaller tap to fill the tank separately is $\mathbf{25}$ hours.
The time taken by the larger tap to fill the tank separately is $\mathbf{15}$ hours.
Question 10. An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11km/h more than that of the passenger train, find the average speed of the two trains.
Answer:
Given:
- Distance between Mysore and Bangalore = 132 km.
- The express train takes 1 hour less than the passenger train for the journey.
- Average speed of the express train = Average speed of the passenger train + 11 km/h.
To Find:
The average speed of the passenger train and the express train.
Solution:
Let the average speed of the passenger train be $x$ km/h.
Then, the average speed of the express train is $(x + 11)$ km/h.
The distance for the journey is 132 km.
We know that Time = $\frac{\text{Distance}}{\text{Speed}}$.
Time taken by the passenger train ($T_p$) = $\frac{132}{x}$ hours.
Time taken by the express train ($T_e$) = $\frac{132}{x + 11}$ hours.
According to the problem statement, the express train takes 1 hour less than the passenger train:
$T_e = T_p - 1$
Or, $T_p = T_e + 1$.
Substituting the time expressions:
$\frac{132}{x} = \frac{132}{x + 11} + 1$
Rearrange the equation to solve for $x$:
$\frac{132}{x} - \frac{132}{x + 11} = 1$
Factor out 132 from the left-hand side:
$132 \left( \frac{1}{x} - \frac{1}{x + 11} \right) = 1$
Find a common denominator inside the parentheses, which is $x(x + 11)$.
$132 \left( \frac{(x + 11) - x}{x(x + 11)} \right) = 1$
$132 \left( \frac{x + 11 - x}{x^2 + 11x} \right) = 1$
$132 \left( \frac{11}{x^2 + 11x} \right) = 1$
$\frac{132 \times 11}{x^2 + 11x} = 1$
$\frac{1452}{x^2 + 11x} = 1$
Multiply both sides by $(x^2 + 11x)$:
$1452 = x^2 + 11x$
Rearrange the terms to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$x^2 + 11x - 1452 = 0$
Now, solve this quadratic equation using the quadratic formula: $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$.
Here, $a = 1$, $b = 11$, $c = -1452$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (11)^2 - 4(1)(-1452)$
$D = 121 + 5808$
$D = 5929$
Apply the quadratic formula:
$x = \frac{-11 \pm \sqrt{5929}}{2(1)}$
We find that $\sqrt{5929} = 77$.
$x = \frac{-11 \pm 77}{2}$
The two possible values for $x$ are:
$x_1 = \frac{-11 + 77}{2} = \frac{66}{2} = 33$
$x_2 = \frac{-11 - 77}{2} = \frac{-88}{2} = -44$
Since the speed ($x$) must be positive, we reject the solution $x = -44$.
Therefore, the average speed of the passenger train is $x = 33$ km/h.
The average speed of the express train is $x + 11 = 33 + 11 = 44$ km/h.
Check:
Time for passenger train = $132/33 = 4$ hours.
Time for express train = $132/44 = 3$ hours.
The express train takes $4 - 3 = 1$ hour less, which matches the given condition.
Final Answer:
The average speed of the passenger train is $\mathbf{33}$ km/h.
The average speed of the express train is $\mathbf{44}$ km/h.
Question 11. Sum of the areas of two squares is 468 m2 . If the difference of their perimeters is 24 m, find the sides of the two squares.
Answer:
Given:
- Two squares.
- Sum of their areas = 468 m2.
- Difference of their perimeters = 24 m.
To Find:
The lengths of the sides of the two squares.
Solution:
Let the side length of the first square be $x$ metres and the side length of the second square be $y$ metres.
Area of the first square = $x^2$ m2.
Area of the second square = $y^2$ m2.
Perimeter of the first square = $4x$ metres.
Perimeter of the second square = $4y$ metres.
According to the first condition, the sum of their areas is 468 m2:
$x^2 + y^2 = 468$
...(i)
According to the second condition, the difference of their perimeters is 24 m. Let's assume $x$ is the side of the larger square (so $x > y$).
Difference of perimeters = Perimeter of first square - Perimeter of second square
$4x - 4y = 24$
Divide the equation by 4:
$x - y = 6$
...(ii)
From equation (ii), we can express $x$ in terms of $y$:
$x = y + 6$
Now substitute this expression for $x$ into equation (i):
$(y + 6)^2 + y^2 = 468$
Expand $(y + 6)^2$ using the identity $(a+b)^2 = a^2 + 2ab + b^2$:
$(y^2 + 2(y)(6) + 6^2) + y^2 = 468$
$(y^2 + 12y + 36) + y^2 = 468$
Combine like terms:
$2y^2 + 12y + 36 = 468$
Move all terms to one side to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$2y^2 + 12y + 36 - 468 = 0$
$2y^2 + 12y - 432 = 0$
Divide the entire equation by 2 to simplify:
$y^2 + 6y - 216 = 0$
Now, solve this quadratic equation for $y$ by factorisation.
We need two numbers whose product is $-216$ and whose sum is $6$. The numbers are $18$ and $-12$.
Split the middle term:
$y^2 + 18y - 12y - 216 = 0$
Factor by grouping:
$y(y + 18) - 12(y + 18) = 0$
Factor out the common binomial factor $(y + 18)$:
$(y + 18)(y - 12) = 0$
Using the Zero Product Property, set each factor equal to zero:
Either $y + 18 = 0 \implies y = -18$
Or $y - 12 = 0 \implies y = 12$
Since $y$ represents the side length of a square, it must be a positive value. Therefore, we reject $y = -18$.
The side length of the second (smaller) square is $y = 12$ metres.
Now find the side length of the first (larger) square using $x = y + 6$:
$x = 12 + 6 = 18$ metres.
Check:
Sides are 18 m and 12 m.
Sum of areas = $18^2 + 12^2 = 324 + 144 = 468$ m2. (Correct)
Perimeters are $4 \times 18 = 72$ m and $4 \times 12 = 48$ m.
Difference of perimeters = $72 - 48 = 24$ m. (Correct)
Final Answer:
The sides of the two squares are $\mathbf{18}$ metres and $\mathbf{12}$ metres.
Example 16 to 18 (Before Exercise 4.4)
Example 16. Find the discriminant of the quadratic equation 2x2 – 4x + 3 = 0, and hence find the nature of its roots.
Answer:
Given:
The quadratic equation is $2x^2 - 4x + 3 = 0$.
To Find:
1. The discriminant of the equation.
2. The nature of the roots of the equation.
Solution:
The given quadratic equation is $2x^2 - 4x + 3 = 0$.
Compare this equation with the standard form of a quadratic equation, $ax^2 + bx + c = 0$.
We have:
$a = 2$
$b = -4$
$c = 3$
The discriminant ($D$) of a quadratic equation is given by the formula:
$D = b^2 - 4ac$
Substitute the values of $a$, $b$, and $c$ into the formula:
$D = (-4)^2 - 4(2)(3)$
$D = 16 - 24$
$D = -8$
The discriminant of the equation is -8.
Now, we determine the nature of the roots based on the value of the discriminant:
- If $D > 0$, the equation has two distinct real roots.
- If $D = 0$, the equation has two equal real roots (one real root).
- If $D < 0$, the equation has no real roots.
In this case, $D = -8$, which is less than 0 ($D < 0$).
Therefore, the quadratic equation $2x^2 - 4x + 3 = 0$ has no real roots.
Final Answer:
The discriminant of the equation $2x^2 - 4x + 3 = 0$ is $\mathbf{-8}$.
Since the discriminant is negative ($D < 0$), the equation has no real roots.
Example 17. A pole has to be erected at a point on the boundary of a circular park of diameter 13 metres in such a way that the differences of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 metres. Is it possible to do so? If yes, at what distances from the two gates should the pole be erected?
Answer:
Given:
- A circular park with diameter AB = 13 m.
- Gates A and B are diametrically opposite fixed points on the boundary.
- A pole is to be erected at a point P on the boundary.
- The difference of the distances from P to A and P to B is 7 m. That is, $|PA - PB| = 7$ m.
To Find:
1. Whether it is possible to erect the pole under the given conditions.
2. If possible, the distances PA and PB.
Solution:
Let P be the point on the boundary of the circular park where the pole is erected.
Let A and B be the two diametrically opposite gates. Then AB is the diameter of the park.
Given, Diameter AB = 13 m.
Since P is a point on the circle and AB is the diameter, the angle subtended by the diameter at any point on the circumference is a right angle.
Therefore, $\angle APB = 90^\circ$.
Triangle APB is a right-angled triangle with hypotenuse AB.
By the Pythagorean theorem:
$PA^2 + PB^2 = AB^2$
$PA^2 + PB^2 = (13)^2$
$PA^2 + PB^2 = 169$
...(i)
We are also given that the difference of the distances from P to A and P to B is 7 m.
$|PA - PB| = 7$
Let's assume PA > PB. Then:
$PA - PB = 7$
From this, we can express PA in terms of PB:
$PA = PB + 7$
...(ii)
Substitute equation (ii) into equation (i):
$(PB + 7)^2 + PB^2 = 169$
Expand $(PB + 7)^2$:
$(PB^2 + 14PB + 49) + PB^2 = 169$
Combine like terms:
$2PB^2 + 14PB + 49 = 169$
Rearrange into the standard quadratic form $ax^2 + bx + c = 0$ (letting $y = PB$ for simplicity):
$2y^2 + 14y + 49 - 169 = 0$
$2y^2 + 14y - 120 = 0$
Divide the entire equation by 2:
$y^2 + 7y - 60 = 0$
To check if it is possible to erect the pole, we need to check if this quadratic equation has real roots for $y$ (which represents the distance PB). We calculate the discriminant $D = b^2 - 4ac$.
Here, $a = 1$, $b = 7$, $c = -60$.
$D = (7)^2 - 4(1)(-60)$
$D = 49 + 240$
$D = 289$
Since the discriminant $D = 289 > 0$, the quadratic equation has real and distinct roots. Therefore, it is possible to erect the pole satisfying the given conditions.
Now, solve the quadratic equation $y^2 + 7y - 60 = 0$ using the quadratic formula or factorization.
Using factorization: We need two numbers whose product is -60 and sum is 7. The numbers are 12 and -5.
$y^2 + 12y - 5y - 60 = 0$
$y(y + 12) - 5(y + 12) = 0$
$(y + 12)(y - 5) = 0$
This gives two possible values for $y$ (which is PB):
$y = -12$ or $y = 5$.
Since $y$ represents the distance PB, it must be positive. Therefore, we reject $y = -12$.
So, the distance PB = 5 metres.
Now find the distance PA using equation (ii):
$PA = PB + 7 = 5 + 7 = 12$ metres.
The distances from the pole P to the gates A and B are 12 m and 5 m respectively.
Final Answer:
Yes, it is possible to erect the pole.
The distances from the two gates A and B to the pole P should be $\mathbf{12}$ metres and $\mathbf{5}$ metres.
Example 18: Find the discriminant of the equation 3x2 – 2x + $\frac{1}{3}$ = 0 and hence find the nature of its roots. Find them, if they are real.
Answer:
Given:
The quadratic equation is $3x^2 - 2x + \frac{1}{3} = 0$.
To Find:
1. The discriminant of the equation.
2. The nature of its roots.
3. The roots, if they are real.
Solution:
The given quadratic equation is $3x^2 - 2x + \frac{1}{3} = 0$.
Compare this equation with the standard form of a quadratic equation, $ax^2 + bx + c = 0$.
We have:
$a = 3$
$b = -2$
$c = \frac{1}{3}$
1. Finding the Discriminant:
The discriminant ($D$) is given by the formula $D = b^2 - 4ac$.
Substitute the values of $a$, $b$, and $c$:
$D = (-2)^2 - 4(3)\left(\frac{1}{3}\right)$
$D = 4 - \frac{12}{3}$
$D = 4 - 4$
$D = 0$
The discriminant of the equation is 0.
2. Nature of Roots:
The nature of the roots is determined by the value of the discriminant ($D$):
- If $D > 0$, there are two distinct real roots.
- If $D = 0$, there are two equal real roots (or one repeated real root).
- If $D < 0$, there are no real roots.
Since $D = 0$, the equation has two equal real roots.
3. Finding the Roots:
Since the roots are real ($D=0$), we can find them using the quadratic formula:
$x = \frac{-b \pm \sqrt{D}}{2a}$
$x = \frac{-(-2) \pm \sqrt{0}}{2(3)}$
$x = \frac{2 \pm 0}{6}$
$x = \frac{2}{6}$
$x = \frac{1}{3}$
The two equal real roots are $\frac{1}{3}$ and $\frac{1}{3}$.
Final Answer:
The discriminant of the equation $3x^2 - 2x + \frac{1}{3} = 0$ is $\mathbf{0}$.
The equation has two equal real roots.
The real roots are $\mathbf{\frac{1}{3}}$ and $\mathbf{\frac{1}{3}}$.
Exercise 4.4
Question 1. Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:
(i) 2x2 – 3x + 5 = 0
(ii) 3x2 – 4$\sqrt{3}$ x + 4 = 0
(iii) 2x2 – 6x + 3 = 0
Answer:
General Concept: Discriminant and Nature of Roots
For a quadratic equation $ax^2 + bx + c = 0$ ($a \neq 0$), the discriminant is given by $D = b^2 - 4ac$.
The nature of the roots depends on the value of D:
- If $D > 0$: Two distinct real roots exist.
- If $D = 0$: Two equal real roots exist (or one repeated real root).
- If $D < 0$: No real roots exist.
If real roots exist ($D \ge 0$), they can be found using the quadratic formula: $x = \frac{-b \pm \sqrt{D}}{2a}$.
Solution (i): $2x^2 - 3x + 5 = 0$
Given equation: $2x^2 - 3x + 5 = 0$.
Comparing with $ax^2 + bx + c = 0$, we have:
$a = 2$, $b = -3$, $c = 5$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (-3)^2 - 4(2)(5)$
$D = 9 - 40$
$D = -31$
Nature of Roots: Since $D = -31 < 0$, the discriminant is negative.
Conclusion: The equation $2x^2 - 3x + 5 = 0$ has no real roots.
Solution (ii): $3x^2 - 4\sqrt{3}x + 4 = 0$
Given equation: $3x^2 - 4\sqrt{3}x + 4 = 0$.
Comparing with $ax^2 + bx + c = 0$, we have:
$a = 3$, $b = -4\sqrt{3}$, $c = 4$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (-4\sqrt{3})^2 - 4(3)(4)$
$D = (16 \times 3) - 48$
$D = 48 - 48$
$D = 0$
Nature of Roots: Since $D = 0$, the equation has two equal real roots.
Finding the Roots: Since real roots exist, we use the quadratic formula $x = \frac{-b \pm \sqrt{D}}{2a}$.
$x = \frac{-(-4\sqrt{3}) \pm \sqrt{0}}{2(3)}$
$x = \frac{4\sqrt{3} \pm 0}{6}$
$x = \frac{4\sqrt{3}}{6}$
$x = \frac{2\sqrt{3}}{3}$
Conclusion: The equation has two equal real roots, which are $\mathbf{\frac{2\sqrt{3}}{3}}$ and $\mathbf{\frac{2\sqrt{3}}{3}}$.
Solution (iii): $2x^2 - 6x + 3 = 0$
Given equation: $2x^2 - 6x + 3 = 0$.
Comparing with $ax^2 + bx + c = 0$, we have:
$a = 2$, $b = -6$, $c = 3$.
Calculate the discriminant $D = b^2 - 4ac$:
$D = (-6)^2 - 4(2)(3)$
$D = 36 - 24$
$D = 12$
Nature of Roots: Since $D = 12 > 0$, the equation has two distinct real roots.
Finding the Roots: Since real roots exist, we use the quadratic formula $x = \frac{-b \pm \sqrt{D}}{2a}$.
$x = \frac{-(-6) \pm \sqrt{12}}{2(2)}$
$x = \frac{6 \pm \sqrt{4 \times 3}}{4}$
$x = \frac{6 \pm 2\sqrt{3}}{4}$
Factor out 2 from the numerator:
$x = \frac{2(3 \pm \sqrt{3})}{4}$
Simplify:
$x = \frac{3 \pm \sqrt{3}}{2}$
The two distinct real roots are $x_1 = \frac{3 + \sqrt{3}}{2}$ and $x_2 = \frac{3 - \sqrt{3}}{2}$.
Conclusion: The equation has two distinct real roots, which are $\mathbf{\frac{3 + \sqrt{3}}{2}}$ and $\mathbf{\frac{3 - \sqrt{3}}{2}}$.
Question 2. Find the values of k for each of the following quadratic equations, so that they have two equal roots.
(i) 2x2 + kx + 3 = 0
(ii) kx (x – 2) + 6 = 0
Answer:
General Concept: Condition for Equal Roots
A quadratic equation $ax^2 + bx + c = 0$ has two equal real roots if and only if its discriminant ($D$) is equal to zero.
The discriminant is calculated as $D = b^2 - 4ac$.
So, the condition for two equal roots is $b^2 - 4ac = 0$.
Solution (i): $2x^2 + kx + 3 = 0$
Given equation: $2x^2 + kx + 3 = 0$.
To Find: Value(s) of $k$ for which the equation has two equal roots.
Solution:
Compare the given equation with the standard form $ax^2 + bx + c = 0$.
Here, $a = 2$, $b = k$, $c = 3$.
For the equation to have two equal roots, the discriminant $D$ must be zero.
$D = b^2 - 4ac = 0$
Substitute the values of $a$, $b$, and $c$:
$(k)^2 - 4(2)(3) = 0$
$k^2 - 24 = 0$
$k^2 = 24$
Take the square root of both sides:
$k = \pm \sqrt{24}$
$k = \pm \sqrt{4 \times 6}$
$k = \pm 2\sqrt{6}$
Conclusion: The values of $k$ for which the equation $2x^2 + kx + 3 = 0$ has two equal roots are $\mathbf{2\sqrt{6}}$ and $\mathbf{-2\sqrt{6}}$.
Solution (ii): $kx(x - 2) + 6 = 0$
Given equation: $kx(x - 2) + 6 = 0$.
To Find: Value(s) of $k$ for which the equation has two equal roots.
Solution:
First, rewrite the equation in the standard quadratic form $ax^2 + bx + c = 0$.
$kx^2 - 2kx + 6 = 0$.
For this to be a quadratic equation, the coefficient of $x^2$ must not be zero, i.e., $k \neq 0$.
Compare $kx^2 - 2kx + 6 = 0$ with the standard form $ax^2 + bx + c = 0$.
Here, $a = k$, $b = -2k$, $c = 6$.
For the equation to have two equal roots, the discriminant $D$ must be zero.
$D = b^2 - 4ac = 0$
Substitute the values of $a$, $b$, and $c$:
$(-2k)^2 - 4(k)(6) = 0$
$4k^2 - 24k = 0$
Factor out $4k$:
$4k(k - 6) = 0$
This implies either $4k = 0$ or $k - 6 = 0$.
If $4k = 0$, then $k = 0$.
If $k - 6 = 0$, then $k = 6$.
However, we established that for the equation to be quadratic, $k \neq 0$. Therefore, we must reject the solution $k = 0$.
The only valid value for $k$ is $6$.
Conclusion: The value of $k$ for which the equation $kx(x - 2) + 6 = 0$ has two equal roots is $\mathbf{6}$.
Question 3. Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m2 ? If so, find its length and breadth.
Answer:
Given:
- A rectangular mango grove.
- Length = 2 $\times$ Breadth.
- Area = 800 m2.
To Find:
1. Whether it is possible to design such a mango grove.
2. If possible, find its length and breadth.
Solution:
Let the breadth of the rectangular mango grove be $b$ metres.
According to the given condition, the length ($l$) is twice its breadth:
$l = 2b$ metres.
The area of a rectangle is given by the formula: Area = Length $\times$ Breadth.
We are given that the Area = 800 m2.
Substituting the expressions for length and breadth:
Area = $(2b) \times b = 800$
$2b^2 = 800$
Divide both sides by 2:
$b^2 = \frac{800}{2}$
$b^2 = 400$
To find the breadth $b$, take the square root of both sides:
$b = \pm \sqrt{400}$
$b = \pm 20$
Since the breadth ($b$) represents a physical dimension (length), it must be a positive value.
Therefore, $b = 20$ metres.
Since we found a positive real value for the breadth, it is possible to design such a rectangular mango grove.
Now, find the length using the relationship $l = 2b$:
$l = 2 \times 20$
$l = 40$ metres.
Check: Length (40 m) is twice the breadth (20 m). Area = $40 \times 20 = 800$ m2. The conditions are satisfied.
Final Answer:
Yes, it is possible to design such a rectangular mango grove.
The length of the grove is $\mathbf{40}$ metres and the breadth is $\mathbf{20}$ metres.
Question 4. Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Answer:
Given:
- The sum of the present ages of two friends is 20 years.
- Four years ago, the product of their ages was 48.
To Find:
1. Whether the given situation is possible.
2. If possible, determine their present ages.
Solution:
Let the present age of the first friend be $x$ years.
Since the sum of their present ages is 20 years, the present age of the second friend is $(20 - x)$ years.
Ages four years ago:
First friend's age = $(x - 4)$ years.
Second friend's age = $(20 - x) - 4 = (16 - x)$ years.
According to the condition, the product of their ages four years ago was 48:
$(x - 4)(16 - x) = 48$
Expand the equation:
$x(16 - x) - 4(16 - x) = 48$
$16x - x^2 - 64 + 4x = 48$
Combine like terms:
$-x^2 + 20x - 64 = 48$
Move all terms to one side to form a standard quadratic equation ($ax^2 + bx + c = 0$):
$-x^2 + 20x - 64 - 48 = 0$
$-x^2 + 20x - 112 = 0$
Multiply the entire equation by -1:
$x^2 - 20x + 112 = 0$
To determine if this situation is possible, we need to check if this quadratic equation has real roots for $x$. We examine the discriminant $D = b^2 - 4ac$.
Compare $x^2 - 20x + 112 = 0$ with $ax^2 + bx + c = 0$.
Here, $a = 1$, $b = -20$, $c = 112$.
Calculate the discriminant:
$D = (-20)^2 - 4(1)(112)$
$D = 400 - 448$
$D = -48$
Since the discriminant $D = -48$ is negative ($D < 0$), the quadratic equation $x^2 - 20x + 112 = 0$ has no real roots.
This means there is no real value of $x$ (the present age of the first friend) that satisfies the given conditions.
Final Answer:
No, the given situation is not possible because the corresponding quadratic equation has no real roots.
Question 5. Is it possible to design a rectangular park of perimeter 80 m and area 400 m2 ? If so, find its length and breadth.
Answer:
Given:
- A rectangular park.
- Perimeter = 80 m.
- Area = 400 m2.
To Find:
1. Whether it is possible to design such a park.
2. If possible, find its length and breadth.
Solution:
Let the length of the rectangular park be $l$ metres and the breadth be $b$ metres.
The perimeter of a rectangle is given by $P = 2(l + b)$.
Given $P = 80$ m:
$2(l + b) = 80$
Divide by 2:
$l + b = 40$
...(i)
The area of a rectangle is given by $A = l \times b$.
Given $A = 400$ m2:
$l \times b = 400$
...(ii)
From equation (i), express length in terms of breadth (or vice versa):
$l = 40 - b$
Substitute this expression for $l$ into equation (ii):
$(40 - b) \times b = 400$
Expand the equation:
$40b - b^2 = 400$
Rearrange the terms to form a standard quadratic equation ($ax^2 + bx + c = 0$, using $b$ as the variable):
$0 = b^2 - 40b + 400$
$b^2 - 40b + 400 = 0$
To determine if this situation is possible, we check if the quadratic equation has real roots for $b$. We examine the discriminant $D = (\text{coefficient of } b)^2 - 4(\text{coefficient of } b^2)(\text{constant term})$.
Comparing with $ax^2 + bx + c = 0$, we have $a = 1$, $b = -40$, $c = 400$.
Calculate the discriminant:
$D = (-40)^2 - 4(1)(400)$
$D = 1600 - 1600$
$D = 0$
Since the discriminant $D = 0$, the quadratic equation has real and equal roots. This means it is possible to design such a rectangular park.
Now, find the roots using the quadratic formula $b = \frac{-(\text{coeff } b) \pm \sqrt{D}}{2(\text{coeff } b^2)}$ or by recognizing the perfect square.
The equation $b^2 - 40b + 400 = 0$ is equivalent to $(b - 20)^2 = 0$.
Taking the square root:
$b - 20 = 0$
$b = 20$
The breadth of the park is $b = 20$ metres.
Now find the length using $l = 40 - b$:
$l = 40 - 20 = 20$ metres.
Since the length and breadth are equal, the park is actually a square.
Check: Perimeter = $2(20 + 20) = 2(40) = 80$ m. Area = $20 \times 20 = 400$ m2. Both conditions are satisfied.
Final Answer:
Yes, it is possible to design such a rectangular park.
The length of the park is $\mathbf{20}$ metres and the breadth is $\mathbf{20}$ metres.

